Quasi-periodic dynamics and the circle maps
In multidimentional dynamical systems with continuous time
oscillations with several different frequencies are possible.
These frequencies depend on system parameters and if their
ratio is an irrational number then quasi-periodic
dynamics appear. Such quasi-periodic orbit with two frequencies
ω1 and ω2 is situated on a
torus. Crosscection of this torus by plane makes a closed curve.
One can parametrize points of this curve by angular coordinate θ.
An orbit starting at a point θn returns again to
the plane in a point θn+1.
In a common case this Poincare map is
θn+1 = θn + f(θn ).
Circle maps
If we keep in f(θ) only the first harmonic,
then we get nonlinear circle maps
θn+1 = θn +
Δ + k sin θn (mod 2π).
Its orbits are defined by winding number
w = limn→ ∞ (θn -
θo )/2πn
note that θ is not truncated to interval (0,2π) here.
For k = 0 the map is a uniform rotation of the circle by angle
Δ, winding number is w = Δ/2π and there are
no fixed points for Δ ≠ 0 . Rational values
w = Δ/2π = p/q with integer p and q
correspond to periodic orbits with "frequency" (p, q).
Such orbits make p revolutions around the circle by q iterations.
Irrational Δ/2π correspond to quasi-periodic orbits. Such
orbit is dense on the circle.
For k < 1 circle maps are monotonic and invertible functions.
There are periodic and quasi-periodic orbits with zero Lyapunov exponents
in this region.
For k > 1 maps are non-monotonic and non-invertible.
There are chaotic orbits with positive Lyapunov exponents in this region.
Bifurcation (isoperiodic) diagram on the (Δ/2π, k/2π) plane.
Click mouse in window to find period p of the point.
Click mouse + <Alt>(<Ctrl>) to Zoom In(Out) 2 times.
Descending to k = 0 and θ/2π = p/q Arnold's tongues
correspond to resonant periodic orbits (p, q).
For k < 1 black regions correspond to quasi-periodic dynamics.
Measure of these regions decreases to zero for k → 1.
For k > 1 in black chaotic see there are windows of regular
dynamics (Milnor's swallow) again.
Periodic orbits
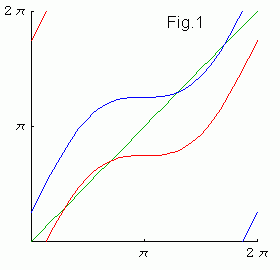 You can see in Fig.1 that for k > 0 the map may have attracting and
repelling fixed points θo . From
You can see in Fig.1 that for k > 0 the map may have attracting and
repelling fixed points θo . From
θo = θo + Δ +
k sin θo
it follows
-sin θo = Δ / k ≤ 1.
Thus for k ≥ Δ there is attracting 0/1 orbit
(it corresponds to the first intersection of the blue curve with diagonal).
For larger k period doubling cascade takes place. Attracting 0/1
orbit loses its stability when derivative of the map
1 + k cos θo = -1
at hyperbola k2 = Δ2 + 4.
The stable 1/1 orbit (it corresponds to the second intersection of
the red curve with diagonal) is determined by
θo + 2π = θo +
Δ + k sin θo.
It exists in the region k ≥ 2π - Δ.
One can expand the second iteration of the circle map for small k
and get for the 1/2 orbit
π - k2/4 < Δ <
π + k2/4.
It agrees well with the bifurcation picture above.
Contents
Previous: "Swallows" and "shrimps"
Next: Baker's map
updated 14 Nov 2006
 You can see in Fig.1 that for k > 0 the map may have attracting and
repelling fixed points θo . From
You can see in Fig.1 that for k > 0 the map may have attracting and
repelling fixed points θo . From