The two-parameter diffeomorphism of Henon is
x' = -x2 + by + a
y' = x.
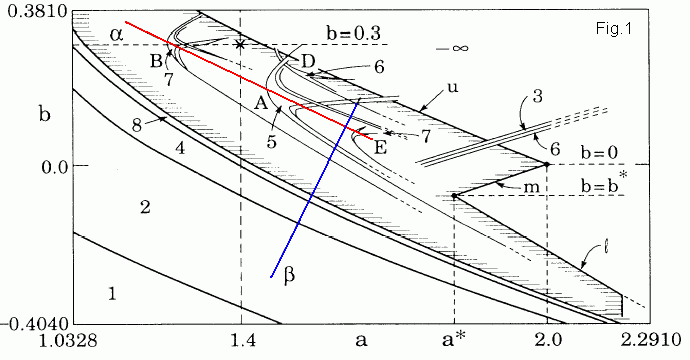
The parameter space of the Henon map is organized in a very regular way.
Complicated pleopodic shrimplike structures are shown below.
Every shrimp consists of a main body of periodicity k plus an
infinite succession of adjacent domains having periods k 2n,
i.e., following a period-doubling route to chaos from the main body k.
Most of shrimps consist of four main legs made of infinite number of
continuous and smouth segments resulting from intersections with legs
from other shrimps.
A striking regularity is that essentially all isoperiodic shrimps appear aligned along a very particular direction α defined by the (red) line b = - 0.583a + 1.025 (see Fig.1 at the bottom). A portion of the line you see above. This pictures is a magnified view of a domain around the 8'-shrimp in the second applet. The dense "foliation" of roughly parallel lines seen to the left and to the right of the 8'-shrimp in the second applet originated from shrimps located almost exclusively along α. There are also a secondary β direction "perpendicular" to all legs going down and a further direction, defined by thouse legs going to the right.
A remark Due to slow convergence near the period doubling bifurcations there are black strips between zones of different periodicities. As since shrimps are rather slow the last applet makes only 300 iterations in every pixel.
[1] J.A.C.Gallas Structure of the parameter space of the Henon map Phys.Rev.Lett., 70, 2714(1993).