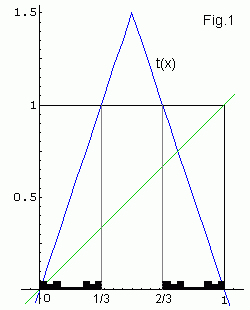
Strange Cantor repeller
Fig.1 shows, how the classic Cantor set emerges in dynamics of the
tent map fc(x) for c = 3 .
As since xo = 0 is an unstable fixed point,
therefore iterations for x outside the [0, 1] interval
diverge to infinity. f(x) maps open interval (1/3,2/3)
beyond [0,1], thus we can throw away these points too. As since
intervals [0,1/3] and [2/3,1] are linear mapped onto
[0,1], therefore we can continue this process ad infinitum.
In every iteration we cut the central one third of an interval. The limit
Cantor set is nowhere dense as since it has holes in any small interval.
The length of all removed intervals is
1/3 + 2/9 + 4/27 + ... = 1/3 ∑n=0,∞
2n / 3n = 1/3 [1 / (1-2/3)] = 1 ,
therefore Lebesque measure (length) of the classic Cantor set is zero.
Its fractal dimension is log2 / log3 .
Cantor set with zero measure will appear for any c > 2.
In the ternary notation after the first iterations all numbers 0.1... are
thrown away and so on. Therefore the Cantor set consists of all ternary
numbers without digit 1. After substitution 2 → 1 one
can see that it is continuum. Rational numbers correspond to unstable
periodic orbits. For a random sequence made of digits 0 and 2
one gets chaotic orbit.
Contents
Previous: Tent map
Next: Quadratic map
updated 1 July 2007
