Chaotic 1D maps
Surprisingly very simple 1D maps yield good model of chaotic systems.
Sawtooth map and Bernoulli shifts
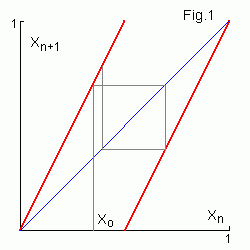 The sawtooth map is determined as
The sawtooth map is determined as
xn+1 = 2xn (mod 1)
where x (mod 1) is the fractional part of x. In the binary
number system multiplying by 2 corresponds to the left shift by
one bit site and taking the fractional part corresponds to the upper bit
truncation. Therefore xn+1 is the Bernoulli shift of
xn
xo = 0.01011 ...
x1 = 0.1011 ...
x2 = 0.011 ...
and so on... The sequence (xo , x1 ...)
is called orbit of the point xo.
Symbolic dynamics and chaos
If the n-th digit after the binary point in xo is
0 (1) then xn lies in the left (right)
half-interval of [0,1]. Thus for the map any orbit is determined
uniquely by its (so , s1 ...) symbolic sequence
σ of visits of these intervals.
For a random symbolic sequence points of corresponding orbit will visit the
left or right half-interval randomly. Existence of continuum of complex
orbits is a sign of chaos.
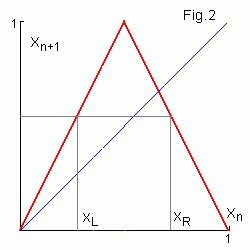
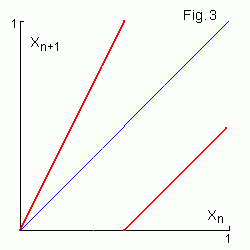
For the continuous noninvertible tent map (to the left) for any
xn one can find preceding xn-1
value lying in the left or in the right half-interval.
Thus in this case it is possible also to make orbit for
any symbolic sequence by reverse iterations of the map.
In general case not all symbolic sequences are allowed. E.g. 11
subsequence is deprecated for the map in Fig.3 to the right.
Unstable orbits and Lyapunov exponent
If xo and yo have k equal
first binary digits then for the sawtooth map while n < k
yn - xn =2n
(yo - xo ) = (yo - xo )
en log 2.
where Λ=log 2 is the Lyapunov exponent for the map.
Thus the distance between two close orbits diverges exponentially with
increasing n.
This property is called sensitivity to initial conditions.
It means that all periodic orbits are unstable too.
Unstable periodic orbits
For the sawtooth map an orbit with rational
xo = p/q is periodic for odd q. E.g. 1/3
orbit has period 2
1/3 → 2/3 → 1/3 ...
and 1/7 orbit has period 3
1/7 → 2/7 → 4/7 → 1/7 ...
For even q an orbit becames periodic eventually, e.g.
1/6 → 1/3 → 2/3 → 1/3 ... or
1/8 → 1/4 → 1/2 → 1 → 1 ...
Therefore there is infinite (countable) set of unstable periodic orbits
and these orbits are dence in [0,1].
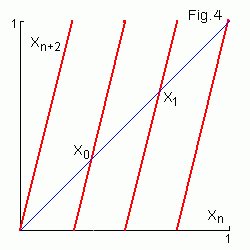 In Fig.4 the second iteration of the map and two points of the period-2
orbit are shown. Period-2 orbit is obtaned from the symbolic sequence
σ= (01) (see Appendix)
In Fig.4 the second iteration of the map and two points of the period-2
orbit are shown. Period-2 orbit is obtaned from the symbolic sequence
σ= (01) (see Appendix)
x0 = 0.0101... = 0.(01) = 1 / 112
= 1/3,
x1 = 0.1010... = 0.(10) =
102 / 112 = 2/3
Two more combinations x2 = 0.(00) = 0 and
x3 = 0.(11) = 1 are fixed points of the map.
Two period-3 orbits are
x0 = 0.001001... = 0.(001) =
12 / 1112 = 1/7,
x1 = 0.(010) = 2/7,
x2 = 0.(100) = 4/7
and x3 = 0.(110) = 6/7,
x4 = 0.(101) = 5/7,
x5 = 0.(011) = 3/7.
Stretching and folding
We may consider the sawtooth map to represent two steps:
(1) uniform stretching of the interval [0,1]
to twice its original length,
(2) left shift of its right half in original position.
The stretching
property leads to exponential separation of the nearby points and hence,
sensitive dependence on initial conditions. The shift property keeps the
generated sequence bounded, but also causes the map to be noninvertible,
since it causes two different xn points to be mapped into
one xn+1 point.
Shadowing
The exponential growth of errors iterating a chaotic dynamical system implies
that a computer generated trajectory for some initial condition will rapidly
diverge from the true orbit due to roundoff errors, so that after a
relatively short time the computer generated orbit (called the
pseudo-trajectory) will have no correlation with the true orbit.
However for given xn of the pseudo-trajectory we can
imagine iterating backwards to find preimage of this point. Since the map is
contracting under inverse iterations, the error decays for backwards
orbits, and the trajectorry remains close to the backwards iteration
of the true trajectory. Existence of a true trajectory that remains
close to the pseudo-trajectory is called shadowing.
Invariant densities
In physical and computer experiments we can set initial conditions only
approximately. But for any finite accurancy of the initial data chaotic
dynamics is predictable only up to a finite number of steps! For such
"turbulent" motions a statistical description may be of more use then
actual knowledge of the true orbits. Therefore we have to trace evolution
of the density of representative points.
For the sawtooth map after every iteration distance between close points
increases two times, thus a smooth density spreads uniformly two times too.
As since all points lay in the bounded [0,1] interval, therefore we
get uniform distribution of the points in the n → ∞
limit. This density is left unchanged by the sawtooth map (it is called
stationary or invariant density). Note that
points of an unstable periodic orbit make singular invariant density.
Ergodicity
If we take random
xo = 0.a1a2a3...
then for any
s = 0.b1b2b3...bk
we can always find somewhere in xo coincident subsequence,
i.e. xn will go close to s and probability of this
"crossing" does not depend on s. Thus every random orbit will go
arbitrary close to any point in [0,1] and cover this interval
uniformly (a funny proof based on mysterious properties of randomness :)
One can use this fact to substitute "time" average <A>
by "ensemble" average (ergodicity)
<A> = ∑n
A(xn) = ∫ A(x) dx.
In general case for a chaotic map
<A> = ∑n A(xn) =
∫ A(x) dμ = ∫ A(x) ρ(x) dx ,
where μ is invariant measure and
ρ(x) is invariant density for the map.
The degenerate circle map
The degenerate circle map
xn = xn-1+Δ
(mod 1) = xo+ nΔ (mod 1)
"wraps" regularly xn points around [0,1] interval
(if one joins 0 and 1 points to make a circle). For a
rational Δ = p/q all orbits are periodic
with period q. For an irrational Δ
every orbit covers [0,1] interval uniformly and dence, therefore one can
introduce constant invariant density again (to calculate averages).
Note, however that all points of the circle [0,1] are displaced by
the map on the same distance Δ. Therefore the distance between
two orbits is constant and density of any ensemble of points keeps its shape.
We have uniform invariant density with no mixing!
Decay of correlations
Average correlation function C(m) for a sequence xk is
C(m) = limn→∞
1/n ∑k=1,n
(xk - <x>)(xk+m - <x>) ,
<x> = limn→∞
1/n ∑k xk .
If invariant measure for a map is known then
C(m) = limn→∞
1/n ∑k(xk - <x>)(f om(xk)
- <x>) = ∫(x - <x>)(f
om(x) - <x>) dμ
E.g. for the degenerate circle map we have
C(m) = 1/12 - δ(1 - δ) / 2 ,
where δ = mΔ (mod 1).
This correlation function oscillates with increasing of m.
For the sawtooth map correlation function is
C(m) = 2-m / 12 .
Thus mixing leads to exponential decay of correlations for large m.
Appendix: Binary code conversion
to rational fraction
Consider decimal fraction at first
0.(3) = 0.333... = 3 (10 -1 + 10 -2
+ 10 -3 + ...) = 3/[10(1 - 1/10)] = 3/9 = 1/3
(formula for the sum of geometric series is used).
In a similar way for binary code
0.(101) = 1012 / 1112 = 5/7 (subscript 2
points the binary system).
Contents
Previous: Chaos in simple maps
Next: Tent map
updated 12 July 2006
 The sawtooth map is determined as
The sawtooth map is determined as


 In Fig.4 the second iteration of the map and two points of the period-2
orbit are shown. Period-2 orbit is obtaned from the symbolic sequence
σ= (01) (see Appendix)
In Fig.4 the second iteration of the map and two points of the period-2
orbit are shown. Period-2 orbit is obtaned from the symbolic sequence
σ= (01) (see Appendix)