Бифуркации удвоения периода
Бифуркации удвоения периода вещественных отображений
При c < 1/4, после касательной бифуркации,
левая неподвижная точка x1 квадратичного отображения
устойчива, пока ее мультипликатор |λ1 | < 1.
При c < -3/4 мультипликатор λ1 =
1 - (1 - 4c)½ < -1, поэтому неподвижная
точка теряет устойчивость и появляется устойчивая орбита с
периодом 2. Это явление называется бифуркацией удвоения периода.
Чтобы проследить за рождением атрактора с периодом 2, рассмотрим
отображение f o2(x) = f(f(x)).
Очевидно, что атрактор fc будет атрактором
fco2 (внизу налево).
При c < -3/4 неподвижная точка теряет устойчивость
и у fco2 одновременно появляется два новых
пеерсечения (внизу направо). Эти точки x3 , x4
образуют орбиту с периодом 2.
При c =-5/4 цикл теряет устойчивость и появляется устойчивая
орбита с периодом 4. Бифуркация удвоения периода называется также
бифуркацией вилки (см. ниже).
Бифуркация удвоения периода на комплексной плоскости

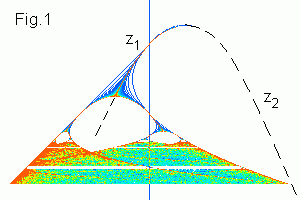
Этот рисунок иллюстрирует бифуркацию на комплексной плоскости.
Пока c меняется от c = 0 до c = -3/4
(внутри главной кардиоиды) атрактор z1
движется от 0 к параболической точке p = -1/2.
Две (комплексные) точки неустойчивой орбиты с периодом 2
z3,4 = -1/2 ± i t,
t = (3/4 + c)½ > 0,
также движутся к p сверху и снизу.
В точке c = -3/4 атрактор встречается с неустойчивой орбитой.
Далее, при c < -3/4 появляются неустойчивая неподвижная точка
и устойчивая орбита с периодом 2
z3,4 = -1/2 ± t,
t = (-3/4 - c)½.
На правой картинке выше показано канторово множество.
Оно получается, если после c = -3/4 смещаться вверх.
Содержание
« Касательные бифуркации
» Бифуркация утроения периода
updated 28 ноября 2013