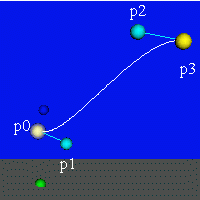
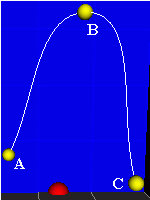
Controls. Press a control point (a ball) to mark it by the white semi-transparent sphere. Then drag mouse in the XY, YZ or XZ plane to move the point. The red ball in the Cardinal demo changes α (you see the α value in the "Status bar").
 
|
Look at interactive cubic Bezier and
Cardinal spline curves VRML demos.
Controls. Press a control point (a ball) to mark it by the white semi-transparent sphere. Then drag mouse in the XY, YZ or XZ plane to move the point. The red ball in the Cardinal demo changes α (you see the α value in the "Status bar"). |
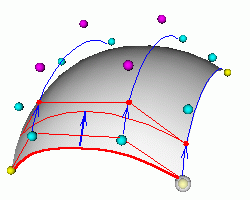

Noninteractive "native" 2x2 order (linear)
Bezier patch.
Isn't it amazing, that this "nonlinear" quadrilateral (its four points don't
belong to a plane) is made of a line moved along two other lines? You see
these lines in the wireframe image.
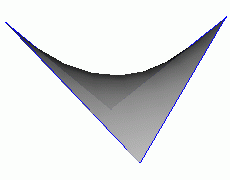
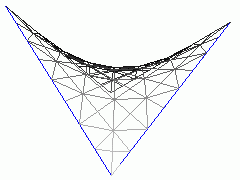
In every point of a Bezier patch we have two tangents directions
A = ∂S(u,v)/∂u and
B = ∂S(u,v)/∂v.
Therefore we get
the normal directions N = [A B] to the surface, i.e.
Nx = (∂Sy
/∂u)(∂Sz /∂v) -
(∂Sz /∂u)(∂Sy /∂v),
Ny = (∂Sz
/∂u)(∂Sx /∂v) -
(∂Sx /∂u)(∂Sz /∂v),
Nz = (∂Sx
/∂u)(∂Sy /∂v) -
(∂Sy /∂u)(∂Sx /∂v).
We can normalize this vector next.
 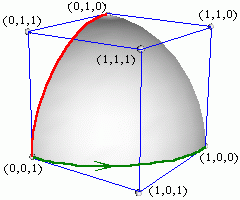
| It is evident, that many useful surfaces can be obtained as a single NURBS patch by tensor product of circular arcs and lines: cone, cylinder, hyperboloid, torus, ring and sphere. |
|
|
If you map a mercator projection photo from NASA
(Maps of the Solar System) on this
sphere, you'll get "SplineGlobe".
I like
Jupiter (it takes 115kb Jpeg from USA,
unfortunately IE says nothing about downloading).
|
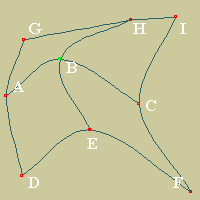
Cardinal spline curve can be generalized easy for 2D regular net of
quadrilateral patches. This generalization is evident for ABC and
EBH splines. Therefore we get the four "boundary" control points
around the B point
(B+-ΔU) ,
(B+-ΔV) , where
ΔU = (C - A)/6 ,
ΔV = (H - E)/6.
The next four "inner" control points are
(B+-ΔU+-ΔV).
It's a hint but not an explanation yet. |