Building of piecewise B-splines is motivated below. You can skip this and go directly to the explanation of B-splines calculations.

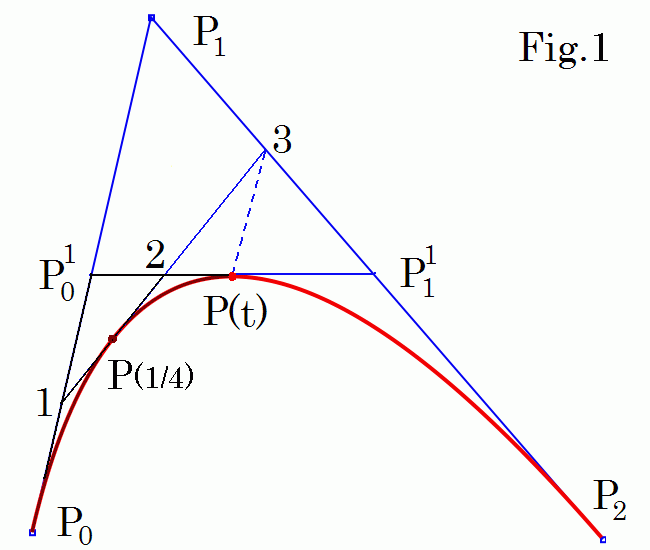
| Any spline point P(t) subdivides Bezier curve in two smaller quadratic splines (with control points P0 , P01, P(t) and P(t), P11, P2 for quadratic splines to the left). The new curves match the original in position, although they differ in parameterization. E.g. for t = 1/2 you see to the left that triangles (1 P01 2) and (3 P(t) 2) are equal and the point P(1/4) of the original spline coincides with the point P(t') of the first small spline for t' = 1/2. |
|
The first derivatives of these two small splines at P(t)
are determined by the P11 P(t) and
P(t) P01 control segments.
Therefore if we drag only P0 or P2
points we get continuous at P(t) curve.
Note that both small splines depend only on its own control points.
In a similar way we get piecewise B-spline with continuous (n - 2)-order derivatives from n-order Bezier spline by subdivision and end control points movement. We can repeat subdivisions to get very complex curve. |
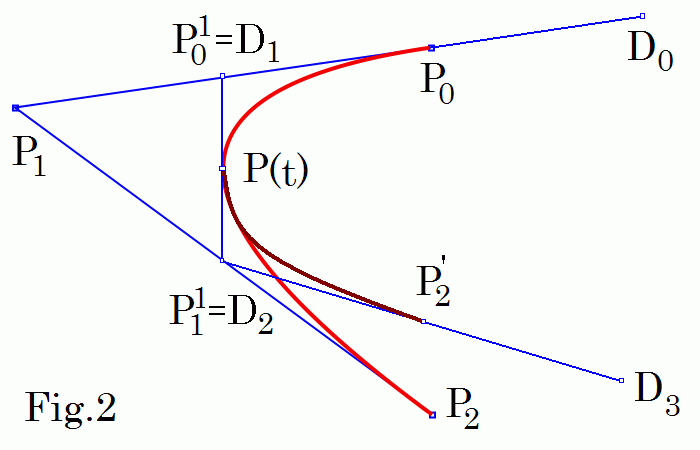
For the spline in Fig.2 we have
n = 3, k = 3, we take the uniform knot vector (-2, -1, 0, 1, 2, 3, 4).
For the first spline segment
D0 = P0 +
(P0 - P1 ), 0 ≤ t ≤ 1
and you can check that
τ11 = (t - t1 )/(t3 -
t1 ) = (t + 1)/2,
P11 =
(1 - τ11)D0 +
τ11D1 =
(1 - t)B0 + t B1 ,
τ21 = (t - t2 )/(t4 -
t2 ) = t/2,
P21 =
(1 - τ21)D1 +
τ21D2 =
(1 - t)B1 + t B2 ,
τ22 = (t - t2 )/(t3 -
t2 ) = t,
P22 =
(1 - τ22)P11 +
τ22P21 =
(1 - t)P11 + tP21.
These are exactly de Casteljau iterations for the first Bezier spline segment
(sorry its control points Bi are itroduced too).
We can "forget" about this lengthy math and use only de Boor control points and
B-spline basis functions in calculations further.