

|
N N < 250
Move
|

|
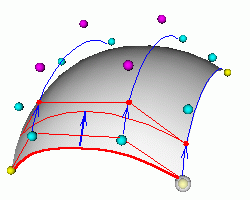
3D spline based modelsThe same cubic Bezier spline patches are used in 3D spline based models. Patches are generated by the old spline-based modelling tool "sPatch". I have found these models in Internet about 10 years ago. |