
CHAPTER 1.
INTRODUCTION TO FIRE CONTROL.
NOTE: Although this chapter is elementary, experience has shown that some
students have a very hazy idea of the fundamentals of fire control. Unless every paragraph of this chapter is understood,
difficulty will be experienced later when studying actual installations. Doubtful points should be cleared up
by consultation with the instructor. For the sake of simplicity some of the definitions given are not rigorous.
FIRE CONTROL.
1. "Fire Control" is a broad term, including the
entire system for controlling a vessel's armament, including personnel, material, methods, etc. It is the purpose of this chapter to
discuss briefly the principles, underlying the fire control systems of ships' gun batteries, and
some of the general features of the systems.
BALLISTIC PROBLEM.
2. By the "ballistic problem" we mean here the
problem of determining how to point the gun with respect to the line joining the gun and the
target. This line is called
the "line of sight".1 In pointer fire the gun is pointed by means of
a sight mechanism which has a telescope attached to it. The problem is to determine how to set the sight so that when the
telescope is pointed at the target the gun will be pointed in the proper direction to
obtain a
hit.2 This requires
that the telescope be offset from the axis of the gun bore vertically and
horizontally. The required vertical
angle is called SIGHT DEPRESSION and the required horizontal angle DEFLECTION.
3. RANGE TABLES.3 For every standard projectile there is a set of one or more
range tables, one for each standard muzzle velocity. Each range table shows, for the various values of range, the ANGLE OF
DEPARTURE (elevation above the horizontal) and
1 This should not be confused with a telescope's
direction, which is the direction in which the telescope is pointed and consequently shifts
with the motion of the ship and the training and elevating of the gun or
director. In fire control literature "line of
sight" is frequently used to mean the telescope's direction, but the
student should learn to recognize the difference.
2 For anti-aircraft fire the fuze setting is also
required.
3 Range tables give
data for surface fire only. Data
for firing at elevated targets
is shown on trajectory curves.
--1--
the DRIFT (lateral deviation in yards due to rotation of the projectile in flight)
for STANDARD CONDITIONS (explained in paragraph 6). Each range table also gives the data necessary to correct for non-standard conditions.
4. SIGHT DEPRESSION or RANGE Setting. When conditions are
standard, sight depression equals the angle of departure shown in
the range table. To facilitate sight setting the SIGHT
BAR scale1 is graduated in RANGE in yards
corresponding to the range table.
Thus, if all conditions are
standard, setting the sight to the
RANGE of the target will automatically apply the required SIGHT
DEPRESSION to the telescope.2 in practice, conditions are never
all quite standard. Furthermore there may be certain errors
requiring correction. Consequently a "BALLISTIC" (correction) must
be calculated and applied to the
setting of the sight.
5. DEFLECTION setting. Deflection is measured in mils, be
cause it is the most convenient
angular measure. It is the angle
which subtends one yard at a distance
of 1000 yards. As stated
in paragraph 3 each range table gives
the DRIFT in yards. The
deflection necessary to overcome the drift may be obtained by dividing the drift in yards by the range in
thousands of yards. If,
for example, the drift, which is always to the right in our service, is 70 yards at 10,000
yards, the corresponding correction
would be left 7 mils. The
deflection drum on the sight is graduated in mils from 0 to 100 or from,
0 to 200, with the arbitrary
zero setting at the mid-point:50 or
100. Settings above the
arbitrary zero cause the gun to be pointed to the right of the
telescope, and vice versa. In the
example just cited, the scale
setting to compensate for drift alone
would be 43 or 93, depending upon whether the arbitrary zero
was 50 or 100. This would be
the setting for firing at 10,000 yards under standard conditions.
Variations from standard
conditions would cause additional lateral
deviations or errors. In practice the DEFLECTION (which is
the
BALLISTIC to be applied to the
mid-point of the deflection scale) is
obtained by computing all of the
lateral deviations in yards,
including the drift, combining them
algebraically, and dividing by
the range in thousands of yards. It should be understood that de
deflection is the angular correction,
not the setting of the
deflection scale. Deflection is
measured in the horizontal plane
through the line of sight.3
1 This scale, which is detachable, is also graduated in
minutes.
2 Not true
for anti-aircraft fire, because the sight depression varies with the
position angle of the target as well as with the range.
3 Strictly speaking this
plane is horizontal only when the line of sight is horizontal, but for surface fire
it may be considered horizontal. For A.A. fire, the deflection ballistic is measured in the slanting plane through the line of sight.
--2--
6. STANDARD CONDITIONS. It has been
stated that range tables
are made up for certain standard conditions, and that the tables
also include data for computing variations from standard conditions. It is these variations,
plus the normal DRIFT, which are
used in obtaining the BALLISTICS in range and deflection to be
applied to the gun sights in pointer fire. The practical computation of ballistic
corrections will be taken up in a later assignment, but it will be well to
briefly indicate here the important STANDARD CONDITIONS:
(a) Gun and target fixed and in the same horizontal plane.
(b) No wind.
(c) A certain "density" of the air.
(d) No variation from designed muzzle velocity.
7. SOLUTION OF THE BALLISTIC PROBLEM. The ballistic problem
is to determine how to point the gun with respect to the line of
sight in order to obtain a hit. As
has been indicated, the ballistic data necessary is given in the appropriate
range table. In order to compute the deviations it is necessary to know the
data variations from standard conditions. To sum up, the following data is needed to solve the problem:
(a) RANGE TABLE
DATA.
(b) TARGET
DISTANCE (RANGE).1
(c) TARGET'S
MOTION(COURSE and SPEED).2
(d) GUN'S MOTION
(own ship's COURSE and SPEED).
(e) WIND'S
MOTION (DIRECTION and FORCE).
(f) AIR DENSITY.
(g) MUZZLE VELOCITY (variation from standard).
The range
table data may be in the form of charts, or cams in computers, etc.
THE FIRE CONTROL PROBLEM.
8. Strictly speaking, the fire control
problem is to deter- mine the TARGET'S POSITION, relative to the gun, and it's
MOVEMENT. In a broader sense, however, when one speaks of the "fire
control problem" he usually means the entire problem of determining the
elevation and train of the gun (and the fuze-setting for an air target) which
will produce a hit. Used in this
broader sense, the term includes the "ballistic problem" referred to
above and the determination of certain other corrections, which will, be discussed later.
9. In
present-day installations the solution of the ballistic problem is so closely
interwoven with the solution of the fire
1 for an elevated target, the POSITION ANGLE must be known.
2 For an aerial target the RATE OF CLIMB must be known.
--3--
control problem that it is sometimes difficult to separate the two. However, for clarity, the elements of
the "fire control problem" will be touched upon.
10. TARGET'S POSITION. For a surface target, the target's
position may be defined by its RANGE
and BEARING. The range may be
measured by rangefinders, or it may
be estimated. In practical
gunnery the gun itself is the best
rangefinder. Although it is
of tremendous advantage to have good
rangefinders, they can never
be depended upon completely, and it
is usually necessary to "spot"
the gun on. Bearing is easily
obtained by direct observation.
Relative bearing is used most, but true bearing is also required,
and is easily obtained. For an air target a third measure is
necessary to define the position of the target. A convenient
one is the "position angle" (sometimes called the
"altitude angle"), which is the angular elevation of the line of sight above the horizontal plane.
11. TARGET'S MOTION. For a
surface target the target's motion
may be defined by its true course and speed. Another way of defining
the direction of the target's motion is by its TARGET
ANGLE,
which is the relative bearing of own ship from the target. The
target angle really defines the target's heading relative to
the
line of sight. For an air target
it is usually more convenient
to
divide the target's motion in the horizontal plane into
two
components: the target's motion (course and speed) through
the air,
and the wind's motion (course and speed, or force and
direction) over the water. As
previously mentioned, a further
measure is necessary to define an air target's motion: the rate
of
climb, which is negative for a dive.
12. The target's motion is estimated to start with. (As a
rule it
is easier to estimate the course than the speed, although
this is
not always the case). With the aid
of observations of
the
changes in range and bearing the rangekeeper assists in
determining more accurately the target's motion. If no rangekeeper
is available, tracking or plotting may be feasible, and should be
of some
assistance. After fire is opened,
observation of the
fall of
salvos may give some indication of the correctness of the
course
and speed set on the rangekeeper.
METHODS OF
CONTROLLING THE ELEVATION AND TRAIN OF THE GUN.
13. Having determined the correct sight depression and deflection, the next
problem is to point the gun accordingly. There
are
several ways of doing this:
14. By GUN SIGHT, as in pointer or master-key fire. The gun
sight
is set to the required sight depression on the angular scale
(or at the range graduation which will give the correct sight
depression)
and deflection scale setting. These settings offset
--4--
the sight
telescopes the" Corresponding angles in elevation and deflection from the
bore, so that if the telescope cross-wires are brought upon the target tire
gun will be correctly elevated and trained.
15. By
DIRECTOR, as ill director fire. The director has
telescopes which can be elevated and trained upon the target. To the director telescope's angle of
elevation is added the sight depression, giving the required GUN ELEVATION
ORDER. To the director telescope's angle of train is added the deflection,
giving the
required GUN TRAIN ORDER. The gun elevation and train
orders are transmitted electrically to the gun, where suitable indicators
enable the trainer and pointer to follow.1
16. It
will be convenient at this point to illustrate the
important angles and their relationships. Figure 1 shows the
vertical plane through gun and target at the instant of firing,
with sights properly set, telescopes properly pointed, and gun
correctly elevated. Plan 2 is a plan view at the same instant.
In connection with Figure 1, the height of the reference
plane is of no significance. It
may be considered to be at any elevation or at several elevations at the same
time.
17. It will be
noted from the above that in director fire the same result is obtained as in
pointer fire, i.e., the gun is elevated above the line of sight at an angle
equal to the sight depression, and trained off from the line of sight by an
angle equal to the deflection. The
director is merely a master sight, capable of controlling and firing the
gun from a distance, with the aid of a suitable electrical transmission
system and a firing circuit.
1 An A.A. director also transmits fuze-setting to the guns.
--5--

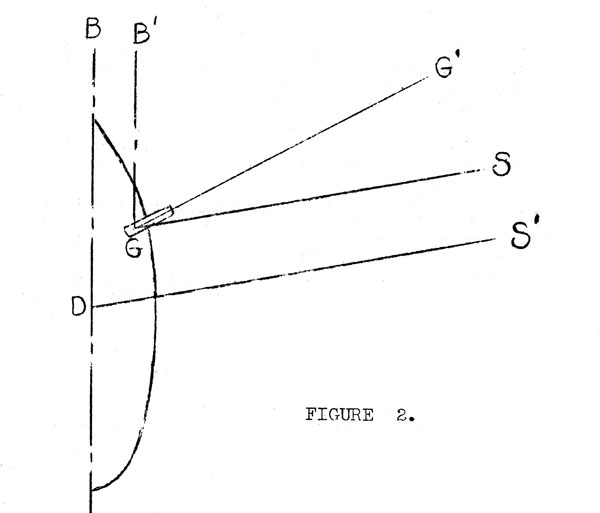
| G |
Gun |
| D |
Director. |
| RP |
The REFERENCE PLANS. (Approximately the plane of the deck). Moves with the
ship in roll and pitch. |
| R'P' |
Plane through the director parallel to the reference plane. |
| GS |
Line of sight between gun and distant target. ALSO in this figure it is
the direction in which the gun telescope is pointed at the instant of
firing. There should be a clear distinction between telescope direction
and line of sight. (See note bottom page 1). In this figure the two
happen to coincide. |
| DS' |
Line from director to distant target. ALSO the director telescope direction
at the instant of firing. For the purpose of this discussion DS' is considered
to be parallel to GS. Strictly speaking DS' makes a small angle with GS, equal
to the vertical parallax. |
| GG' |
Axis of the bore of the gun when properly laid. |
| P'DS' |
Angle of elevation of director telescope above the reference plane = DIRECTOR
CORRECTION = PGS. |
| SGG |
Sight depression. |
| PGG' |
Gun angle. If gun is properly laid it also equals the GUN ELEVATION ORDER, which
is sight depression plus director correction. (Gun elevation order
is what is sent to the guns. Gun angle is the actual elevation of the
gun above the reference plane. When the gun is properly laid
these two angles are equal except for small corrections made at the gun). |
--6--
| G |
Gun |
| D |
Director. |
| GS |
Line of sight. |
| DS' |
Line of sight from director to distant target. It is treated
here as being parallel to GS. Actually the two lines make an angle with each other
called the horizontal parallax. |
| BBS' |
Relative bearing of target from director. Neglecting horizontal parallax it is
equal to the relative bearing of the target as measured at the gun
(B'GS). |
| SGG' |
Deflection. In this case it is left, or negative. |
| B'GG' |
Gun train angle. If the gun is properly trained it also equals the GUN TRAIN
ORDER, which is the algebraic sum of the relative target bearing and the
deflection. |
--7--
INDIRECT FIRE.
18. Another method of controlling the gun is by INDIRECT
FIRE. In pointer and director fire a telescope is pointed at
the target and the gun oriented with respect to the telescope's
direction. In indirect fire the target cannot be
seen from the
ship, and some other reference must be used. In addition some
observer (usually
aircraft) outside the ship must spot the gun
on. Two methods of using indirect fire are possible:
Use another point of aim, whose position with
respect to target and own ship is known. Deter
mine the offset angles, in elevation and train,
between the line from own ship to target, and the
line from own ship to the point of aim. Point a
director at the point of aim' and apply the offset angles.
Use some kind of artificial horizon as standard
in elevation, and a stabilized standard of reference in train, such as a gyro compass. Use an offset from North in train, if using the gyro
compass, equal to the algebraic sum of the TRUE
target bearing and the deflection.
Note that in indirect fire, as in the cases of pointer
and director fire, the same fundamental requirement is met: In effect,
the gun is pointed the required angle above the line of sight
from gun to target, and trained off the required angle, even though the target
actually can't be seen.
THE ELEMENTARY DIRECTOR SYSTEM.
19. Fire control systems vary as to detail, but all have
certain features in common, as illustrated in Figures 3 and 4 and
explained in the following paragraphs:
20. Angles of elevation are measured above the reference
plane,
which is approximately the plane of the deck. By director
to
checks in elevation the scale at each gun and director is
made to read the angle of elevation above the reference plane.
The DIRECTOR CORRECTION is the angular elevation of the
director telescope above the reference plane.
21. Angles of train are measured as relative bearings from
the bow to the right through 360°. By
director checks in train the
scale at each gun and director is made to read correctly.
22. Every director installation includes a rangekeeper.
Rangekeepers vary greatly in their design, but for the present
we may consider them to be not only keepers of the range, as the
name implies, but also computers which solve at least a part of
--8--
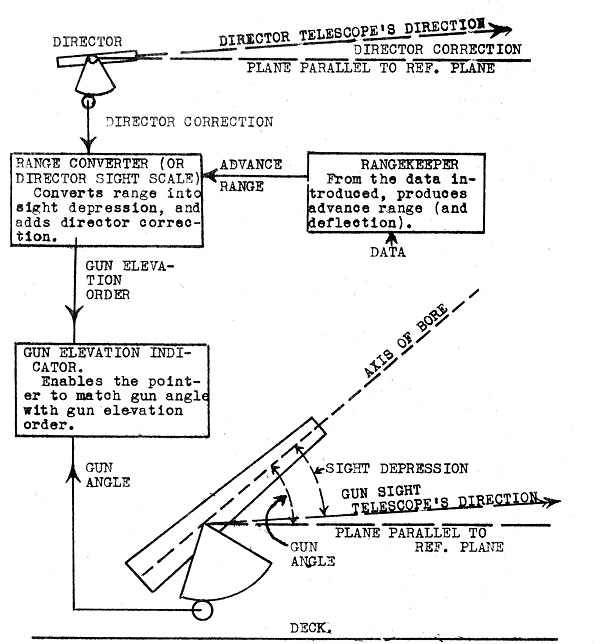
Figure 3.
ELEMENTARY DIRECTOR SYSTEM (ELEVATION).
Note: This figure represents the relationships of reference
plane, axis of bore, and telescopes' directions with respect
to each other and to the ship when ready to fire,
but not necessarily at the instant of firing, i.e. the telescopes may or may
not be pointing at the target.
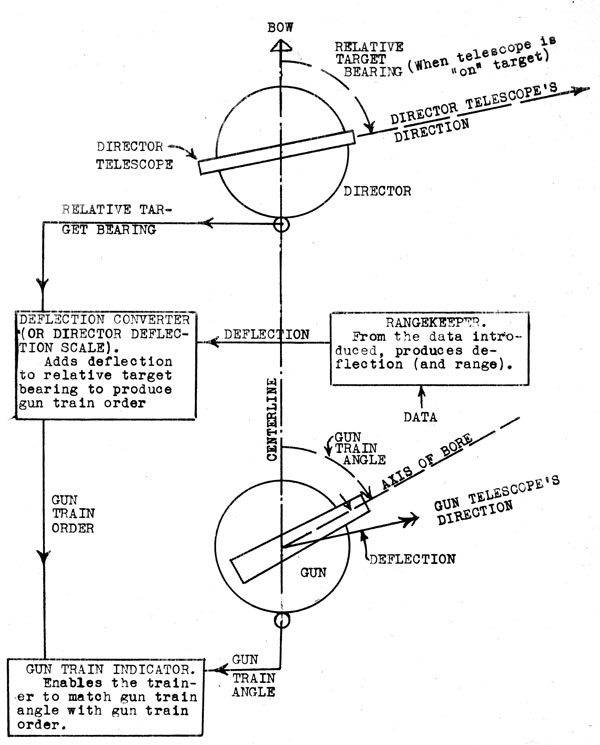
Figure 4.
ELEMENTARY DIRECTOR SYSTEM (TRAIN)
the complete fire control and ballistic problem when the proper data are
introduced. The outputs of a
rangekeeper are, in general, ADVANCE RANGE and DEFLECTION. Advance range is the
best estimate of the actual target distance at the present time, plus all range corrections necessary to produce a hit.
23. Converters. Converters are used in main
battery installations.
In the later installations they are
housed in the rangekeeper itself,
form an integral part of the rangekeeper, and are not thought of as separate mechanisms. However, in thinking of
an elementary director system, it is
well to consider this as a
separate instrument. Converters convert advance range in
yards to sight depression in minutes,
and add the director correction, the
output being GUN ELEVATION ORDER. Either housed
in the same instrument case, or
separate from it is a device
for adding deflection to relative
target bearing to obtain GUN TRAIN ORDER.
24. In secondary battery installations and in some others
there are no plotting rooms, and no range converters. In place
of the
range converter there is a sight scale connected to the
director telescope, which works like a gun sight. The range
scale is
graduated in yards to agree with the corresponding
sight
angles from the range tables, similarly to the graduations
of a gun
sight. When a range is set on the
sight, the
director
pointer's telescope is depressed accordingly. When
the
director telescope is elevated to the target the gun elevation order increases, causing the guns to elevate above the
line of
sight just as though the gun sight had been set and the
gun
pointer had looked through his telescope and elevated until
he was
"on". The effect is the
same as though a range converter
were
used: the director telescope when
on the target will be
elevated
above, or depressed below the reference plane by an
angle
equal to, the director--correction, but the order which
goes out
to the guns will be the algebraic sum of the sight
depression
and-the director correction. In
such an installation
the "director correction" is automatically taken care of, and
need not even have a name, so far as the operating personnel
are
concerned.
25. Gun Indicators. At each gun
are located two indicators.
The GUN
ELEVATION INDICATOR receives the gun elevation order
and the
actual gun angle to which the gun is elevated above the
standard
reference plane. When pointers in
the indicator are
matched,
the gun is elevated to the required angle. Similarly
the GUN
TRAIN INDICATOR receives the gun train order and the
gun train angle, and shows when the two are matched.
26. CORRECTORS. Installations
vary as to the corrections
made and
the manner of making them. This
subject will be taken
up in
Chapter 2.
--9--
Table of Contents
Next Chapter (2)
Transcribed and formatted by Thomas Wildenberg



