3000. RELATIVE MOTION AND THE USE OF THE MANEUVERING BOARD.
INTRODUCTION.
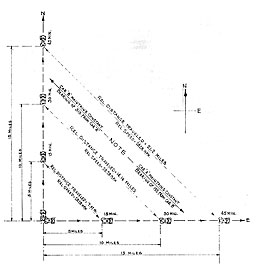
Each of us is familiar with geographical movement. A man walking across the street moves geographically from a position on one side of the street to a position on the opposite side, passing through successive positions in the street while crossing. A motorist driving from one city to the next, along a winding highway or over a succession of roads and crossroads, makes the same kind of geographical movement--just a bit more complicated --as the man crossing the street. There is a second kind of movement that is as useful as geographical movement in many instances, particularly in CIC. It is the movement that takes place between two objects each making its own geographical movement. Consider the case of two motorists leaving the same point and driving North and East respectively, each performing a geographical movement of his own. If each drives at 20 miles per hour, he will travel 5 miles in the first 15 minutes. But after 15 minutes, the two motorists will be 7 miles apart, and the one who has driven East will be Southeast of the other motorist. This movement that has taken place between them--leaving the same spot and being 7 miles apart after 15 minutes--is different from the geographical movement of either motorist; it is the result of their geographical movements.
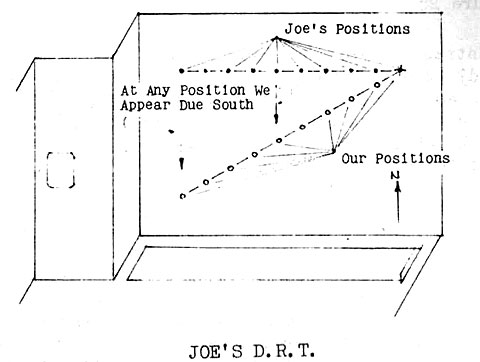
If they follow their respective routes for another 15 minutes, each will have traveled 10 miles over the earth from the starting point. Yet at the end of this time the two will be separated by 14 miles, with the motorist who has gone East still directly Southeast of the one who has gone North. After the first 15 minutes the two were separated 7 miles in a SE/NW line; now they are 14 miles apart, still in a SE/NW line. If they drive for another 15 minutes, they will be separated about 21 miles, although each will have driven only 15 miles. It is apparent that each, insofar as the other is concerned, is moving 7 miles farther away every 15 minutes. He is accomplishing this separation in a definite direction. Let us place ourselves in the position of the motorist who has driven North. We see the motorist who has driven East getting farther and farther away from us, always to the Southeast of us, and getting 7 miles farther away to the Southeast every quarter hour. Aside from what either of us is doing with respect to the earth, it is apparent that there is a movement occurring between the other motorist and us: he is getting 28 miles farther Southeast of us every hour. In addition to the motion of the individual cars, one to the North, the other to the East, there is also a motion existing (See Figure 24) between the two. This motion is the RELATIVE MOTION between them.
RELATIVE MOVEMENT.
Relative motion or movement is concerned with the movement between two objects. Movement, in turn, is concerned with direction, distance, and speed. Since the movement under discussion here is relative, each of the above factors also become relative.