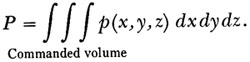Chapter 12
ATTACKS BY AIRCRAFT
| 12.1 |
GENERAL STATEMENT OF PROBLEM |
The general theory of aircraft attacks can be approached along the lines used in considering surface craft attacks. Although the details of the two
subjects differ widely, many of the basic theoretical ideas developed in the previous chapter are applicable in the present one. Furthermore, the general
type of operational data available and the system used in assessing attacks are the same. As before, we shall first give a brief overall description of
the problem and then proceed to detailed considerations. In both cases, a priori and a posteriori aspects will be treated.
Aircraft are greatly superior to surface craft in locating submarines on the surface, but their effectiveness for underwater search and tracking is
very limited.23 As a result, aircraft are primarily of value in attacking submarines sighted on the surface. Many attacks will actually be delivered
while the submarine is still fully or partly surfaced, but the rapidity with which a submarine can crash dive as the aircraft closes to attack means
that attacks shortly after submergence must also be considered.24
When an aircraft has made contact with a surfaced submarine (either visually or by radar), it must next get into a favorable position to make an
attack. Since the target is small, it is necessary to get down to a low altitude for maximum accuracy. The target will, however, usually submerge on
sighting the aircraft in order to escape attack, and therefore the approach must be made in such a way as to obtain the maximum element of surprise
and limit, as much as possible, the degree to which the submarine can submerge prior to attack. During the approach the course and speed of the
submarine must be estimated so that allowance can be made for target motion. When the proper position has been reached, the aircraft releases its
weapons. These may be either rockets or bombs. As in the case of surface craft attacks, the problem is to release the weapons so that they will
reach a point beneath the surface at the same time the submarine reaches that point. (See Figure 1.) From a knowledge of the characteristics of
the weapons and of the position of the submarine at the time of attack, it is possible to determine where the weapons should strike the water to
be effective. The probability of success will then depend on the accuracy with which the correct target position is estimated, on the errors made
in placing the weapons in the desired position, and on the lethality of the weapons used.
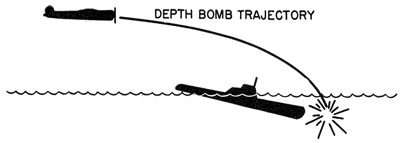 |
FIGURE 1. Aircraft depth-bomb attack. |
The above factors will be considered in detail in the balance of this chapter. We shall first give a theoretical discussion and follow with a
consideration of operational results. Since depth bombs have so far been the primary aircraft weapon against the submarine, operational experience
is most extensive for this weapon. Certain other phases of operational results cannot be discussed at this time because highly classified information
is involved. Hence much of the following detailed discussion will be confined to the depth bomb and it should be considered as an example of methods
of evaluation rather than as a complete examination of the subject of aircraft attack weapons and tactics.
| 12.2 |
THEORETICAL DISCUSSION OF FACTORS DETERMINING THE SUCCESS OF ATTACKS |
The factors determining the probability of success in an aircraft attack can be grouped in the same two general categories as were involved in surface craft attacks: attack
errors and weapon lethality. Attack errors, in turn, may be subdivided as follows:
--127--
- Errors in estimating submarine position.
- Errors caused by variation in the behavior of individual missiles.
- Aiming errors.
If weapons are released while the submarine is still visible, errors in estimating target position will be restricted to misestimates of target
motion from the time of release to the time of impact or explosion (the "blind time").25 For rockets such movement of the submarine is so small that
no allowance is ordinarily made for it. For depth bombs, the time from release to explosion will be on the order of 5 sec or so, depending on exact
conditions of attack, in which time a submarine can travel only about one-half its length. It is fairly easy to make allowance for such changes in
target position and errors will be negligible.
On the other hand, if the submarine submerges completely before attack, there is a longer blind time and the uncertainty of submarine position
will increase with increase in this blind time, in the manner discussed in Chapter 11. The effect of a long blind time will be especially serious
in aircraft attacks since there is no information as to the target's course and speed except visual estimation, and the barrage which can be dropped
by aircraft is too small to cover radical changes of speed and course on submerging. The expansion of the possible area in which the submarines may
be at the end of a given number of seconds after submergence is shown in Figure 2. This is based on the turning characteristics of the 500-ton German
U-boat and assumes that speed may vary from 3 to 7 knots. It will be noticed that the possible area remains very small for the first 15 sec or so and
then increases rapidly until, at the end of 1 minute, it is about 270,000 sq ft.
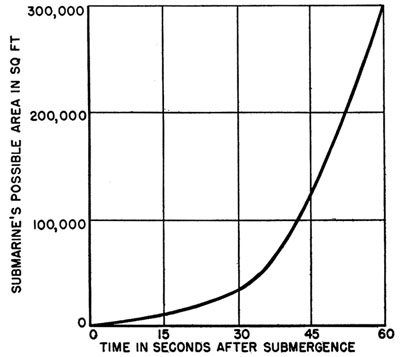 |
FIGURE 2. Submarine evasion area as a function of time. |
From the above discussion, it is evident that attack errors due to misestimation of target position increase so rapidly with time after submergence
that the probability of success quickly approaches zero. For Class A attacks, which arc defined as those made on visible submarines or on submarines
submerged less than 15 sec, the submarine's position is quite well known. For Class B attacks, which are attacks on submarines submerged between 15
and 30 sec, the submarine's position has become uncertain. For attacks made still later, the probable error in estimating submarine position has become
extremely large. A priori, therefore, we would expect a much greater degree of success in Class A attacks than in others, the probability diminishing
rapidly for Class B and later attacks. An accurate, quantitative a priori evaluation is not available, but one based on operational experience will be
given later to bear out the above qualitative conclusion.
The obvious method of reducing errors of the type just discussed is to reduce blind time, that is, to make as many attacks as possible on visible
submarines or, at least, on those within the Class A category. It is therefore important to employ tactics designed to achieve the greatest amount of
surprise in the attack. Some of the factors involved are speed of aircraft, correct patrol altitude, approach from cloud cover, use of camouflage to
avoid visual detection of aircraft, and use of countermeasures to search receivers to avoid detection of radar emissions.26 It is also advantageous
to make attacks in locations where submarines are less alert, that is, to surprise them in areas where aircraft attack is not expected. In addition
to such measures, the number of favorable attacks can be increased by avoiding attacks which involve too great a blind time and which therefore have
a negligible probability of success so that time and weapons may be conserved for possible future
--128--
opportunities against Class A targets. The effect of all such measures in increasing the proportion of Class A attacks is somewhat difficult to
evaluate a priori, but we shall show later, from operational experience, the overall improvement which resulted from emphasis on the importance of
prompt attacks involving the maximum element of surprise.
The second class of attack errors mentioned above involved those due to variation in the behavior of individual missiles. In aiming a given weapon,
it is necessary to assume a certain behavior after it leaves the aircraft. Variations from this normal will, of course, occur. Depth bombs, for example,
will vary in their fall through air and in their underwater travel. There will also be a variation in the depth at which they explode. Similarly, rockets
will vary in flight path and in underwater trajectory. Such deviation will, of course, decrease the accuracy of the attack. Errors of this type can only
be reduced by improved design of weapons. Extensive practical tests and analyses of operational results will often prove of value in determining the
effectiveness of improved design.
As an illustration of the size of errors of the type just discussed, the following estimates for depth and contact bombs are quoted in Table 1.
TABLE 1. Variation of individual missiles.
(Aircraft speed 100-200 knots, altitude 50-200 ft.)
| Type of bomb |
Probable deviation along aircraft course (feet) |
Probable deviation perpendicular to aircraft course (feet) |
| Round-nose U.S. depth bomb |
17 |
17 |
| Flat-nose U.S. depth bomb |
7 |
7 |
| Contact bomb (Hedgehog or Mousetrap) |
3½ |
0 |
Considerations of target position and weapon characteristics determine the point on the water at which the weapons must strike to be effective. Errors
in placing them in the desired position may be called aiming errors. This is the third subdivision of attack errors mentioned above. Aiming errors are
commonly measured with relation to the aircraft's course. Errors along its course are called range errors, while those perpendicular to its course are
called line errors.
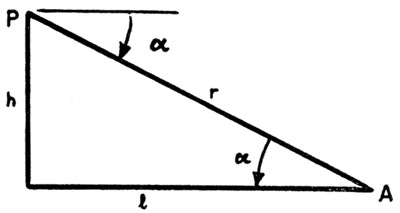 |
FIGURE 3. Geometry of horizontal bombing. |
Line errors are caused by failure of the pilot to fly in a straight line directly over the aim point, while range errors are due to release of bombs
at the wrong moment, or, in the case of rockets, to improper altitude of the plane at the moment of firing. The size of these errors will depend on the
conditions of attack, on the skill of the pilot and bombardier, and on the accuracy of the bomb or rocket sight used.
As an example of aiming errors and methods of reducing them, consider the problem of delivering an attack with depth bombs. The pilot flies as nearly
as possible straight across the aim point and thus controls the line error. The problem as far as range is concerned is, then, to determine the proper
moment for release of the bombs. For a horizontal attack, the geometry of the situation is simple. In Figure 3, P represents the position of the plane
at moment of release of the center bomb of the stick, A represents aim point, h is altitude, r slant range, and 1 horizontal range
(in feet). The angle α is the angle between the line PA and the horizontal. Then, disregarding air resistance, the center bomb will travel forward a
distance 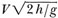 ft, where V is plane velocity in feet per second. Hence correct release will occur
when
ft, where V is plane velocity in feet per second. Hence correct release will occur
when 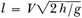 or
or 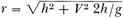 or when α has the value determined
by the relationship tan α=h/l. Hence the aiming problem in range can be solved for a given altitude by selecting either the proper slant
range, horizontal range, or angle between the horizontal and line from aircraft to aim point. Use of r is indicated for radar bombsights since slant
range can be determined by radar. Use of the angle α is involved in using the reflector gunsight which enables determination of this angle. In addition
to the above means it is possible to utilize the rate at which the angle α is changing, as is done in the angular velocity bombsight. Whereas other
methods are sensitive to correct determination of speed and altitude this latter method is relatively insensitive to errors in such factors.
or when α has the value determined
by the relationship tan α=h/l. Hence the aiming problem in range can be solved for a given altitude by selecting either the proper slant
range, horizontal range, or angle between the horizontal and line from aircraft to aim point. Use of r is indicated for radar bombsights since slant
range can be determined by radar. Use of the angle α is involved in using the reflector gunsight which enables determination of this angle. In addition
to the above means it is possible to utilize the rate at which the angle α is changing, as is done in the angular velocity bombsight. Whereas other
methods are sensitive to correct determination of speed and altitude this latter method is relatively insensitive to errors in such factors.
The aircraft will not necessarily make a level approach to the target. On sighting the submarine the plane will normally be at a rather high search
altitude and must lose altitude to make the attack.
--129--
Hence it is often natural for the plane to make the bombing run while still in a glide. In a glide attack the formulas for determining release point are
somewhat more complex than in horizontal bombing, but similar methods of controlling range errors can be used. There is also the possibility of using the
plane's motion in pulling out of a glide to release the bombs, a method known as toss-bombing.
Commonly used during the recent war, because of the lack of suitable bombsights, was the so-called seaman's eye method of bombing. This term is applied
to bombing without a sight in which the pilot releases bombs at the proper moment by instinct gained over long periods of practice.
Aiming errors, for a given method of aiming, will vary widely with such factors as type of aircraft, degree of training and individual ability of pilots
and bombardiers, conditions of attack, etc. It is not possible, therefore, to quote figures of general applicability. The performance of a typical TBF squadron
trained in glide bombing at ASDevLant gives an indication of the order of magnitude of such errors in training and of the effect of practice in reducing them.
During a 3-week period, each pilot made about 100 practice attacks on a towed target, using a glide angle of about 15 degrees and aiming by means of a
reflector sight. The mean point of impact [MPI] for all attacks was 62 ft over in range and 8 ft right in line. Probable error about the MPI was 80 ft in
range and 30 ft in line.27
During the 3-week period the MPI in range decreased from about 135 ft to 18 ft. The MPI in line did not improve. The probable error about the MPI
decreased from 98 ft to 40 ft in range and from 38 ft to 25 ft in line. It is evident, therefore, that training brought the MPI effectively on the target
and reduced dispersion about the target very noticeably. Improvement was still continuing after 100 practice attacks per pilot.
After the 3-week training period in glide bombing the squadron spent a week in horizontal bombing by seaman's eye. The MPI was 31 ft over in range
and 1 ft right in line, with probable errors about the MPI of 66 ft in range and 14 ft in line. Since these results were obtained after the extensive
practice in glide bombing, a direct comparison of overall results by the two bombing methods is not fair, but it can be judged that range errors in
horizontal bombing were about 20 per cent greater than in glide bombing while line errors were only about half as great.
The improvement possible by use of an accurate sight is suggested by the fact that tests at ASDevLant with the BARB (angular velocity) sight showed
a probable error of only 16 ft in range. It was found that very little training was required. Similar improvement in rocket accuracy by use of proper
sights is indicated by ASDevLant tests. Using the reflector sight with prescribed sighting allowance, mean deviation of about 10 mils in range was
achieved by the best trained squadrons, the RASP (automatic vector) sight gave 8 mils, and toss-rocketing, 6.3 mils.
Operational errors usually proved considerably greater than those obtained in practice attacks. These will be discussed in the next section.
The effect of the three types of errors discussed above on the success of an attack can only be determined by considering such errors in connection
with the lethality of a given weapon. We shall therefore next discuss weapon lethality and then illustrate the combination of attack errors and weapon
lethality in determining a priori probabilities of success.
From a general point of view, the concept of commanded volume discussed under surface craft attacks is applicable to aircraft attacks. For example,
if a stick of depth bombs is dropped, each bomb will have around it a commanded volume constructed by the method previously given. The probability of
success will be given by equation (1).
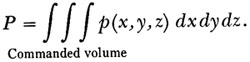 |
Equation (1) |
where the function p(x,y,z) is the probability that the center of the submarine is at position x,y,z and is determined by the attack errors. The
probability of a hit on the pressure hull by a salvo of rockets could be similarly determined; in this case the commanded volume of each rocket would
be the solid generated by moving along the underwater trajectory of the rocket an area equal to the cross section presented by
--130--
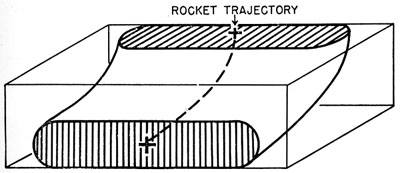 |
FIGURE 4. Commanded volume of antisubmarine rocket. |
the pressure hull for the given angle of attack.28 (See Figure 4.)
Because of the effect of blind time on bombing errors, however, aircraft attacks must be made on surfaced or nearly surfaced submarines to be successful.
It is convenient, therefore, to eliminate submarine depth as a variable in the problem and to make probability calculations on the basis of an assumed
depth or a small range of equally probable depths. This enables us to replace the concept of commanded volume by one of lethal area.
This method may be illustrated by considering an attack against a German 500-ton U-boat by an aircraft dropping a stick of depth bombs of the type
used in World War II. For such attacks, a fixed depth setting of 25 ft was ultimately adopted. This is approximately correct for the average Class A
submarine if we consider all depths of the pressure hull's center between 6½ ft (for surfaced U-boats) and 40 ft (for U-boats down 15 sec) as
equally likely. Since bombs set for 25 ft actually exploded somewhat deeper, we shall assume an effective depth setting of 30 ft for our illustration.
(This is probably about correct for the best United States fuze developed in World War II.)
Considering, then, only Class A attacks made with this effective depth setting and assuming all depths between 6/2 ft and 40 ft as equally likely,
the lethal area may be determined as follows. The average distance from the center of the pressure hull measured perpendicular to the submarine's keel
within which a depth bomb must explode to be lethal is found from Figure 5. The bomb will be effective provided the center of the pressure hull lies
within the shaded area of the diagram, that is, within a radius of the point of explosion equal to the lethal radius of the bomb plus the radius of the
pressure hull. In the diagram, a lethal radius of 17½ ft has been used; this is about correct for a TNT-filled, 350-1b United States depth bomb.
From this diagram the average width for which such a depth bomb is effective can be easily determined; it comes out as about 40 ft. In other words the
charge must be at a distance, measured perpendicular to the keel, of not over 20 ft from the center of the pressure hull. Consider next the distance
measured parallel to the submarine's keel within which such a bomb must explode to be lethal. For the 500-ton U-boat, allowing for variation in diameter
at the ends and also for the fact that the charge may be effective somewhat ahead or aft of the hull, it is found that a bomb with a 17½-ft lethal
radius should be effective if it explodes not more than 95 ft ahead or astern of the pressure hull's center, based on the same considerations as to depth
as were previously used.
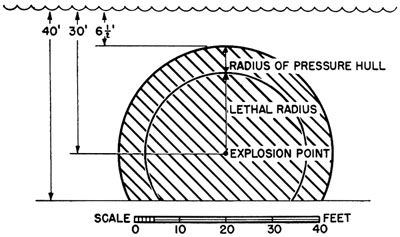 |
FIGURE 5. Depth coverage. Depth bomb, lethal radius = 17½ ft. Average width covered = 40 ft. |
It follows, therefore, that for the kind of bomb and submarine considered there is a lethal area 190 ft long and 40 ft wide on the surface of the
water with its center directly above the center of the pressure hull, as shown in Figure 6. Thus if a bomb explodes below this area at the assumed
depth of 30 ft, it will sink the submarine.29 The probability that this will occur depends, of course, on the attack errors.
Another point of view is to consider this lethal area as surrounding each bomb, with its long dimension in the direction of the U-boat's keel.
Then if the center of the submarine lies within the lethal area of any one of the bombs of the stick, the attack will be
--131--
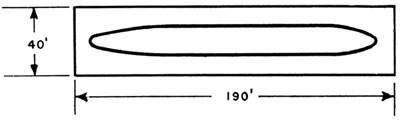 |
FIGURE 6. Lethal area for depth bomb (TNT-filled 350-Ib) bomb). |
successful. As before, the probability of this occurring may be found by consideration of the attack errors.
Similar methods of approach can be used for other types of bombs. The problem for rockets is also analogous. Under given conditions of submarine depth
and angle of attack, considerations of the underwater trajectory of the rocket during the period for which speed is adequate for penetration will indicate
how far short of the target, in range, it can strike and still be lethal30 The aspect presented by the submarine will determine permissible variation in
line. For example, in a beam attack on a surfaced submarine with a 15° glide angle, it has been estimated that a Model 5 rocket will be lethal if it strikes
the water not more than 67 ft short of the submarine nor more than 80 ft to either side-that is, under these conditions the lethal area is 67 x 160 ft, as
shown in Figure 7.
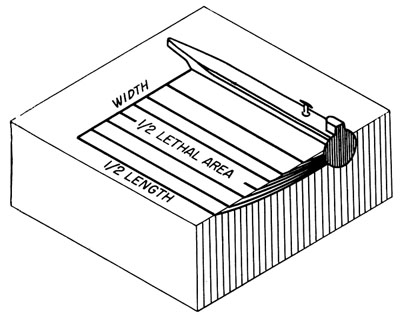 |
FIGURE 7. Lethal area for rocket against surfaced submarine (beam attack). |
| 12.2.3 |
Probability of Success |
We can illustrate the method of combining attack errors and weapon lethality to determine a priori probabilities of success by considering a stick
of four depth bombs under the same assumptions as were used in our illustration of lethal area. For simplicity let us assume an attack made from directly
on the beam and disregard individual dispersion of the bombs. We shall further assume that probable attack errors in range and line are 120 ft and 65 ft,
respectively, and that these arc normally distributed about the U-boat's center.31 Under such assumptions it is evident that the most effective stick
spacing is 40 ft, since with this spacing the lethal area of each bomb just touches that of each of the adjacent bombs and there arc no gaps or overlaps
in the total lethal area of the four bombs. We have, then, an effective lethal area for the whole stick of 160 ft along the aircraft's track and 190 ft
perpendicular to the aircraft's track, as shown in Figure 8. If the center of the submarine lies within this total area the attack will be a success.
Based on the assumed probable error of 120 ft in range, the curve showing the probability that the center of the submarine will be a given distance in
range from the center of the stick is simply the normal distribution curve shown in Figure 9. The probability that the center of the submarine will be
within 80 ft of the center of the stick in range is, therefore, the area under this curve from x = -80 to x = +80, namely, 0.35.
A similar calculation of the probability that the center of the submarine will be within 95 ft of the center of the stick in line, based on
the assumed probable
 |
FIGURE 8. Area for stick of four depth bombs. |
--132--
TABLE 2. Characteristics of bombs.
| Type |
Explosive |
Nose |
Lethal
radius |
Depth of
explosion |
Dispersion |
Along
aircraft
course |
Perpendicular
to aircraft |
350-lb depth bomb
(explosive 250 lb) |
TNT |
Flat |
17½ ft |
30 ft |
7 ft |
7 ft |
| Round |
17½ ft |
30 ft |
17 ft |
17 ft |
| Torpex |
Flat |
22 ft |
30 ft |
7 ft |
7 ft |
650-lb depth bomb
(explosive 450 lb) |
TNT |
Flat |
25 ft |
30 ft |
7 ft |
7 ft |
| Round |
25 ft |
30 ft |
17 ft |
17 ft |
650-lb depth bomb
(explosive 450 lb) |
TNT |
Flat |
Contact |
Contact |
3½ ft |
0 |
error of 65 ft in line, gives 0.68. The actual probability of success depends on the occurrence of both these events and is therefore 0.35 x 0.68 = 0.24;
in other words, under the assumptions made the stick of bombs has a 24 per cent chance of killing the submarine.
The calculation is considerably more complex if individual bomb dispersion is taken into account and if angles of attack intermediate between 0 degree
and 90 degrees to the submarine's course are considered. The above example, however, illustrates the basic theory involved. We shall next examine the results
of some a priori calculations of this sort.
 |
FIGURE 9. Probability that center of submarine will be a given distance in range from center of stick. |
Such calculations serve several purposes. They make it possible to determine optimum tactics for the use of a given weapon and answer such questions as:
what is the best angle of attack, what is the best spacing for bombs in a stick, etc. More fundamentally, they make it possible to compare the expected
effectiveness of different basic types of weapons and of different models of a given type. Such comparisons are of value in determining which weapons
should be used and often suggest profitable improvements in their design. A priori probability calculations may also be used to study the effect of
accuracy in the use of a given weapon and show to what extent improvement in probability of success is possible through improvement in accuracy.
Finally, such calculations predict what should be expected from operational results and are useful in evaluating such results. We shall illustrate
the above points by considering the use of bombs in Class A attacks against the German 500-ton U-boat with the same assumptions as to the depth of
the pressure hull's center as were used in discussing lethal area (i.e., all depths between 6½ ft and 40 ft are considered equally likely).
Results will be shown for the basic types of United States bombs used in World War II. Table 2 summarizes the assumptions made as to their characteristics.
(Weight is given in round figures - individual types of bombs vary somewhat in weight.)
Assumptions as to probable aiming errors (including probable submarine position error) are shown in Table 3 for beam attacks and lengthwise attacks.
(Consistent values have been used for intermediate angles of attack.)
On the above assumptions the effect of stick spacing on probability of success is illustrated in Figure 10 for 350-1b, TNT-filled, round-nose depth
bombs. On the basis of similar calculations for various angles of attack, the curves shown in Figure 11 can be obtained. It will be noted from Figure 11
that there is a
TABLE 3. Assumed bombing errors for Class A attacks.
| |
Probable error
in range |
Probable error
in line |
| Beam attack |
120 ft |
65 ft |
| Lengthwise attack |
135 ft |
20 ft |
--133--
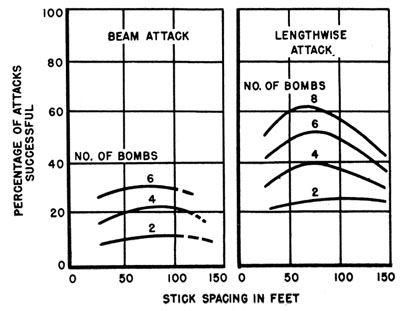 |
FIGURE 10. Probability of sinking as a function of stick spacing, 350 lb, round-nose depth bombs,
TNT- filled. |
wide variation in optimum spacing for a two-bomb stick according to angle of attack and only small variation for other stick sizes. Figure 10, however,
shows that the actual effect of stick spacing on probability of success is almost negligible for a two-bomb stick and is greatest for the longer sticks. In
other words, for cases where the optimum varies, the importance of using the optimum value is small, whereas for cases for which use of an optimum value is
important nearly the same value is optimum for all angles of attack. It follows therefore that an overall value of about 75 ft for all angles is quite
satisfactory.
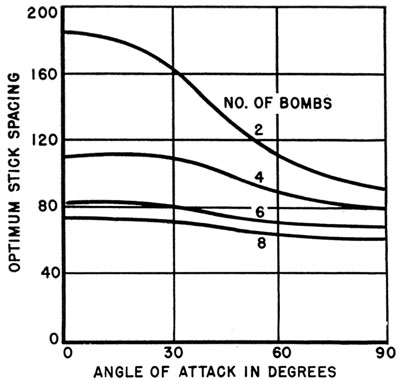 |
FIGURE 11. Optimum stick spacing as a function of angle of attack, 350-1b, TNT-filled, round-nose depth bombs. |
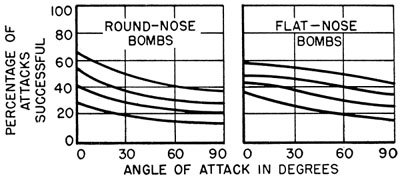 |
FIGURE 12. Probability of sinking as a function of angle of attack, with best stick spacing for each angle. |
This is an important conclusion, since varying the stick spacing for each attack would result in complication and delay. It can also be seen from
Figure 10 that even for larger sticks the use of values deviating somewhat from the 75-ft value suggested will be quite acceptable.
(Similar conclusions have been found for flat-nose bombs.)
The effect of angle of attack on success is illustrated in Figure 12 for the round-nose depth bombs just considered and for
corresponding flat-nose bombs. It is apparent that angles along the submarine's track give the best probability of success. The improvement possible by
selecting this angle makes it worthwhile to do so wherever convenient. However, the gain is not sufficient to warrant delay in attack for this purpose.
The above results are merely illustrative since the effect of stick spacing and angle of attack will vary with the type of bomb considered and the
assumptions made in the calculations, but it is felt that the conclusions may safely be applied to low-level depth bomb attacks on Class A submarines.
We shall now proceed to a comparison of the different types of bombs listed in Table 2, averaging results over all angles of attack and using the best
stick spacing at each angle.
Such a comparison is most instructive if made on a weight-for-weight basis, as has been done in preparing the curves shown in Figure 13.
One fact is immediately evident from these curves. There is a great gain in effectiveness with number of bombs dropped, regardless of type. This
means that it is important to drop a sufficient number in the first attack to secure a high probability of success. Withholding bombs is not warranted
unless there is a very good chance of making a second Class A attack. For example, if the chance of a second attack is less than 25 per cent, as many as
ten 350-1b bombs are justifiably expended on the first attack.
--134--
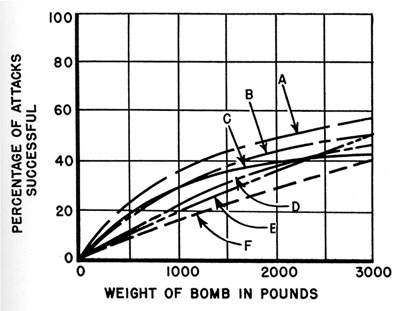 |
FIGURE 13. Probability of sinking as a function of weight of bombs in stick for various types of bombs.
Averaged over all angles of attack with optimum stick spacing at each angle.
- 350-1b Torpex flat-nose;
- 350-1b TNT flat-nose;
- contact;
- 350-1b TNT round-nose;
- 650-lb TNT flat-nose;
- 350-1b TNT round-nose.
|
A comparison of the results according to type of bomb illustrates several important points. These may be summarized as follows.
- A comparison of the curves for round-nose bombs with the corresponding curves for flat-nose bombs indicates the marked improvement achieved by
decreasing the dispersion in underwater trajectories of individual bombs from 17 ft to 7 ft through proper design of the bomb.
- A comparison of the curves for 350-1b bombs with those for 650-lb bombs shows that on a weight-for-weight basis the smaller bombs should be markedly
superior for all sizes of bomb stick. Although the 350-1b depth bomb is the lightest used by the United States Navy, it is not necessarily optimum. A
study, under the same assumptions, of the British 265 lb bomb (weight of Torpex, 193 lb) showed somewhat better results on a weight-for-weight basis. It
is quite possible that still lighter bombs might be effective, but the results would depend on various factors, such as the percentage of explosive weight
to total weight, weight of equipment required to drop longer sticks, etc.
- A comparison of the curve for the 350-lb Torpex flat-nose bomb with the curve for the corresponding TNT-filled bomb shows the value of using a more
powerful explosive. Improvement of lethal radius for a given weight of bomb by means of an improved explosive is a very effective means of increasing the
lethality of attack.
- The curves show that for the bombs considered (and under the assumptions made) the 350-lb flat-nose, Torpex-filled depth bomb is superior for any given
weight of bombs dropped. For the other types, the contact bomb of Hedgehog type appears superior for weights under about 1000 lb, but this may be only an
apparent advantage. Depth bombs exploding outside lethal range may still damage the submarine, whereas a near miss with a contact bomb does no damage.
Furthermore, the extra weight required by more numerous bomb racks for small contact bombs will also lessen their advantage. Since only Class A attacks
have been considered, it may seem that the advantage of contact bombs in covering all possible submarine depths has been disregarded in our analysis.
Actually, however, consideration of later attacks would add little to the probabilities for contact bombs because of the uncertainty of submarine position.
The above results are based on fixed assumptions as to aiming errors. The effect of such errors is illustrated in Figure 14
for a stick of six 350-1b Torpex flat-nose depth bombs. Probability of sinking has been averaged over all angles of attack with best stick spacing for each angle.
Results are shown according to the probable range error for a beam attack. Line errors for beam attacks and both line and range errors for other
angles of attack have also been varied so as to be proportional to the range error indicated, using the relationship reflected in
Table 3. This curve shows very strikingly the importance of accuracy in aiming. For range errors under 50 ft, an attack is almost certain
to be successful, but the probability
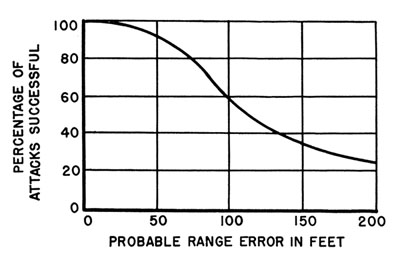 |
FIGURE 14. Probability of sinking as a function of the expected errors in bombing for six 350-1b
Torpex flat-nose depth bombs. |
--135--
TABLE 4. Effect of degree of submergence at attack.
(Independent attacks by United States aircraft.)
Degree of
Submergence |
July-Dec 1942 |
Jan-July 1943 |
| No. |
%A-D |
%A or B |
No. |
%A-D |
%A or B |
| Fully surfaced |
17 |
41 |
24 |
52 |
37 |
23 |
| Decks awash |
7 |
29 |
0 |
5 |
40 |
20 |
| Stern and/or conning tower |
22 |
32 |
5 |
25 |
20 |
4 |
| Periscope |
3 |
0 |
0 |
2 |
0 |
0 |
| Down 0-15 sec |
38 |
3 |
3 |
11 |
18 |
9 |
| Down 15-30 sec |
25 |
4 |
4 |
11 |
0 |
0 |
| Down 30-45 sec |
12 |
0 |
0 |
4 |
0 |
0 |
| Down over 45 sec |
22 |
0 |
0 |
5 |
0 |
0 |
| Other |
9 |
8 |
8 |
33 |
30 |
21 |
| TOTAL |
167 |
5 |
5 |
150 |
25 |
15 |
drops off rapidly thereafter. For errors of about 125 ft it is down to about 50 per cent. The value of an effective bomb sight is clearly indicated by
these figures.
A priori probabilities of success with eight solid-head rockets, for effective angles of attack, are of about the same order of magnitude as corresponding
probabilities of success with six depth bombs using the seaman's eye method of aiming. For example, using aiming errors (standard deviation) of 35 mils in
azimuth and 25 mils in elevation (which are about twice the errors obtained in practice), the probability of a kill on a Class A U-boat at 400-yd range in a
20 degree dive with eight rockets is about 50 per cent. This is about the same as the probability shown in Figure 14 for six United States Torpex flat-nose
depth bombs with a range error of 120 ft. The above comparison, of course, involves certain specific assumptions as to aiming errors and weapon characteristics.
Future improvement in aiming methods and, possibly, in weapon design may affect the two weapons differently and it is, therefore, not possible to conclude which
will ultimately be the better. Actually, it is not necessary to decide this point since they are complementary in nature. Depth bombs are effective at all angles
of attack and for attacks made shortly after submergence, while rockets are restricted to angles near the beam and to use on visible submarines. On the other
hand, rockets are light in weight and provide an effective weapon for small planes which cannot carry bombs. They also provide an additional punch for bombing
planes, giving them something like twice the effective weapon capacity with only a small increase in load.
| 12.3 |
OPERATIONAL EXPERIENCE |
Actual results achieved in aircraft attacks during World War II verify many of the a priori conclusions drawn in the previous section. First to be considered
is the importance of making prompt attacks and of using a depth setting appropriate for such attacks.
| 12.3.1 |
Effect of Degree of Submergence at Attack |
Table 4 shows the results achieved by independent United States aircraft attacks in the Atlantic and Mediterranean during the last half of 1942 and the
first 7 months of 1943. The percentage of A-D attacks (U-boat sunk or damaged) and that of A or B attacks (U-boat sunk or probably sunk) are shown for each
period according to the degree of submergence at attack.
The marked improvement in overall results from the first period to the second is clearly associated with a much greater proportion of attacks on fully
surfaced U-boats. The detailed breakdown for each period shows quantitatively the correctness of the conclusion reached in our theoretical discussion as to
the decrease in probability of success with increase in degree of submergence.
| 12.3.2 |
Importance of 25-ft Depth Setting |
When the United States entered World War II, depth settings of 50 ft were common. By the latter half of 1942, the importance of a shallower setting
had been recognized and the usual depth setting was
--136--
25 ft. However, 39 attacks during July-December 1942 involved 50-ft settings. These resulted in 3 per cent A-D assessments as compared with the
overall figure of 11 per cent shown in the above table. During the first half of 1942, when the deeper setting was generally used, a total of 174
independent aircraft attacks on U-boats in the United States Strategic Area resulted in only 4.6 per cent A-D assessments. Undoubtedly the deeper
setting was at least partly responsible for this poor showing. Operational experience thus bears out clearly the importance of making prompt attacks
with a shallow depth setting.
Since the 25-ft setting for United States depth bombs actually produced explosion at depths greater than 25 ft on the average, the improvement
noted above was only a partial realization of that which was theoretically possible. Tests indicated that during the period January-July 1943 the
current United States depth bomb when set for 25 ft actually fired at depths between 27 and 64 ft, with an average of about 40 ft. On the other hand,
the British depth bomb fired at very nearly the correct depth. A comparison of operational results with the two different bombs should therefore
indicate the advantage of the one which exploded at the desired depth. Such a comparison is made in Table 5. The British figures are based on daylight
attacks on fully or partly surfaced U-boats during the period April-0ctober 1943. The United States figures are based on attacks for the period
January-July 1943, including all degrees of submergence. To compensate for the inclusion of attacks on submerged submarines, United States attacks
assessed A-D (sunk or seriously damaged) are considered successful. (Since 72 per cent of the United States attacks were on fully or partly visible
U-boats, whereas kills were only 54 per cent of the total A-D assessments, this actually results in overcompensation, and the comparison is therefore
somewhat too favorable to the United States depth bomb.)
TABLE 5. Operational results with different depth bombs.
| British Depth Bomb |
| Theoretical results |
Operational results |
|
No. of
bombs |
Per cent
kill |
No. of
bombs
(average) |
Per cent
kill |
Ratio of
operational
to
theoretical |
| 2 |
20.5 |
2.5 |
20 |
98% |
| 4 |
34 |
4 |
28 |
82% |
| 6 |
51 |
5.9 |
37 |
73% |
| 8 |
57 |
7.8 |
55 |
96% |
United States Depth Bomb |
| Theoretical results |
Operational results |
|
No. of
bombs |
Per cent
kill |
No. of
bombs
(average) |
Per cent
kill |
Ratio of
operational
to
theoretical |
| 2 |
23.5 |
2.4 |
11 |
47% |
| 4 |
41.5 |
4 |
27 |
65% |
| 6 |
54 |
5.7 |
33 |
61% |
| 8 |
66 |
8.3 |
36 |
55% |
It can be seen from the above that the British bomb gave results close to expectation, whereas the United States bombs averaged a little over
half the expectation.
| 12.3.3 |
Importance of Bombing Errors |
Next to be considered are operational bombing errors and improvement in them due to practice and the use of bombsights. As to the actual size
of such errors a British analysis of 43 photographed daylight attacks made by seaman's eye on visible submarines during the period March-October
1943, showed mean errors about the conning tower of 141 ft in range and 71 ft in line. These errors were not uniformly distributed about the conning
tower. Systematic errors in estimating submarine motion were apparently negligible but there was a systematic overshoot along the aircraft track
resulting in an MPI which was 86 ft over in range. The MPI in line was reasonably near the conning tower, i.e., 13 feet left. The errors showed
considerable variation with angle of attack; the measured results are shown below. It was found that the photographic sample was biased since track
attacks with small line error rarely gave satisfactory photographs because explosion plumes obscured the U-boat. Therefore, the line error in track
attacks shown in Table 6 is somewhat too large. Attacks on submarines which had submerged less than 15 sec before attack gave average errors of 192
ft in range and 73 ft in line. The sample, however,
TABLE 6. Operational bombing errors (visible U-boats).
| |
Average
line error (feet) |
Average
range error (feet) |
| Beam |
75 |
124 |
| Quarter |
75 |
155 |
| Track |
66 |
139 |
--137--
was small and results are not very reliable. Comparison of those measured errors with those assumed in Table 3 for theoretical calculations shows reasonable agreement, with the
assumed errors somewhat advantage smaller than those actually made in operations.
The effect of practice in reducing bombing errors cannot be evaluated explicitly from operational results because of the lack of sufficient
photographs. The importance of continued practice is, however, illustrated by Coastal Command experience for the period May-December 1943.
Table 7 shows a comparison of results for this period according to amount of practice.
TABLE 7. Effect of practice on attack accuracy.
| |
Bomb aimers who had
dropped less than 10
practice bombs during
preceding month |
Bomb aimers who had
dropped more than 10
practice bombs during
preceding month |
| Good attacks |
51% |
65% |
| Moderate attacks |
13% |
20% |
| Bad attacks |
36% |
15% |
The effect of a bombsight on bombing accuracy is illustrated by British experience with the Mk III (angular velocity) sight. An analysis of results
through June 1944 showed average range errors about the conning tower of 130 ft as compared to 180 ft for seaman's eye bombing under the same conditions.
Average line errors were 33 ft as compared to 56 ft by seaman's eye, though there is no reason to expect an improvement in line error. There was an
increase in lethality of about 35 per cent in kills and 60 per cent in kills and damage. These results are based on a very small sample (32 attacks,
16 photographs) and therefore are not conclusive; however they do show the bombsight to be a promising development.
| 12.3.4 |
Importance of Large Bomb Stick |
Operational experience has clearly borne out the advantage of dropping large sticks of bombs. For example, in the period from July 1942 to
July 1943 United States results for depth bombs set at 25 ft were as given in Table 8.
TABLE 8. Success of attack for different sizes of stick.
(United States aircraft, July 1942-July 1943.)
| Number of bombs |
Percentage A-D assessments |
| 1-3 |
13% |
| 4 |
21% |
| 5-12 |
34% |
| 12.3.5 |
Results with Rockets |
Operational results with rockets are not very extensive. Almost all United States rocket attacks were made in connection with other types of attacks
so that no specific conclusions can be drawn from them. British attacks, however, demonstrate that rockets have been effective. For example, during the
period May-December 1943, 18 attacks on Class A U-boats (of which 14 were fully surfaced) resulted in 33 per cent A or B assessments and an additional
22 per cent C, D, and E assessments. The 33 per cent kills is in fair agreement with the 50 per cent expected figure quoted in our theoretical discussion
when consideration is given to the fact that the average firing range was 600 yd instead of 400 yd, the average number of projectiles 7.3 instead of 8,
and the average glide angle 17 degrees to 25 degrees instead of 20 degrees. The above figure of 33 per cent kills is comparable to the result previously
shown for British depth-bomb attacks on visible submarines, using six bombs, for the period April-October 1943, namely 37 per cent. (See Table 5.) It is
the same as the figure previously shown for six United States depth bombs (based on A-D assessments, all attacks). There seems little doubt, therefore,
that rockets are of about the same degree of effectiveness as depth bombs, although, as pointed out previously, each weapon has its own particular advantages.
--138--
Table of Contents
Previous Chapter (11) * Next Chapter (13)
Footnotes
Transcribed and formatted for HTML by Rick Pitz for the HyperWar Foundation