


Whenever electrons flow through a conductor, a magnetic field will develop around that conductor. This effect is called electromagnetism. Magnetic fields affect the alignment of electrons in an atom, and can cause physical force to develop between atoms across space just as with electric fields developing force between electrically charged particles. Like electric fields, magnetic fields can occupy completely empty space, and affect matter at a distance.
Fields have two measures: a field force and a field flux. The field force is the amount of "push" that a field exerts over a certain distance. The field flux is the total quantity, or effect, of the field through space. Field force and flux are roughly analogous to voltage ("push") and current (flow) through a conductor, respectively, although field flux can exist in totally empty space (without the motion of particles such as electrons) whereas current can only take place where there are free electrons to move. Field flux can be opposed in space, just as the flow of electrons can be opposed by resistance. The amount of field flux that will develop in space is proportional to the amount of field force applied, divided by the amount of opposition to flux. Just as the type of conducting material dictates that conductor's specific resistance to electric current, the type of material occupying the space through which a magnetic field force is impressed dictates the specific opposition to magnetic field flux.
Whereas an electric field flux between two conductors allows for an accumulation of free electron charge within those conductors, a magnetic field flux allows for a certain "inertia" to accumulate in the flow of electrons through the conductor producing the field.
Inductors are components designed to take advantage of this phenomenon by shaping the length of conductive wire in the form of a coil. This shape creates a stronger magnetic field than what would be produced by a straight wire. Some inductors are formed with wire wound in a self-supporting coil. Others wrap the wire around a solid core material of some type. Sometimes the core of an inductor will be straight, and other times it will be joined in a loop (square, rectangular, or circular) to fully contain the magnetic flux. These design options all have an effect on the performance and characteristics of inductors.
The schematic symbol for an inductor, like the capacitor, is quite simple, being little more than a coil symbol representing the coiled wire. Although a simple coil shape is the generic symbol for any inductor, inductors with cores are sometimes distinguished by the addition of parallel lines to the axis of the coil. A newer version of the inductor symbol dispenses with the coil shape in favor of several "humps" in a row:

As the electric current produces a concentrated magnetic field around the coil, this field flux equates to a storage of energy representing the kinetic motion of the electrons through the coil. The more current in the coil, the stronger the magnetic field will be, and the more energy the inductor will store.

Because inductors store the kinetic energy of moving electrons in the form of a magnetic field, they behave quite differently than resistors (which simply dissipate energy in the form of heat) in a circuit. Energy storage in an inductor is a function of the amount of current through it. An inductor's ability to store energy as a function of current results in a tendency to try to maintain current at a constant level. In other words, inductors tend to resist changes in current. When current through an inductor is increased or decreased, the inductor "resists" the change by producing a voltage between its leads in opposing polarity to the change.
To store more energy in an inductor, the current through it must be increased. This means that its magnetic field must increase in strength, and that change in field strength produces the corresponding voltage according to the principle of electromagnetic self-induction. Conversely, to release energy from an inductor, the current through it must be decreased. This means that the inductor's magnetic field must decrease in strength, and that change in field strength self-induces a voltage drop of just the opposite polarity.
Just as Isaac Newton's first Law of Motion ("an object in motion tends to stay in motion; an object at rest tends to stay at rest") describes the tendency of a mass to oppose changes in velocity, we can state an inductor's tendency to oppose changes in current as such: "Electrons moving through an inductor tend to stay in motion; electrons at rest in an inductor tend to stay at rest." Hypothetically, an inductor left short-circuited will maintain a constant rate of current through it with no external assistance:
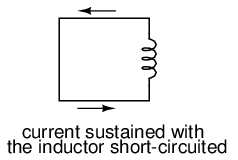
Practically speaking, however, the ability for an inductor to self-sustain current is realized only with superconductive wire, as the wire resistance in any normal inductor is enough to cause current to decay very quickly with no external source of power.
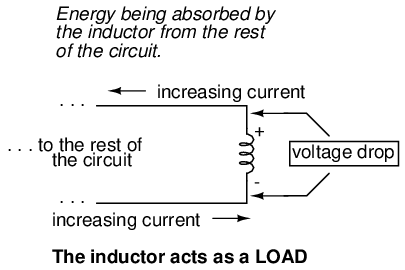
When the current through an inductor is increased, it drops a voltage opposing the direction of electron flow, acting as a power load. In this condition the inductor is said to be charging, because there is an increasing amount of energy being stored in its magnetic field. Note the polarity of the voltage with regard to the direction of current:
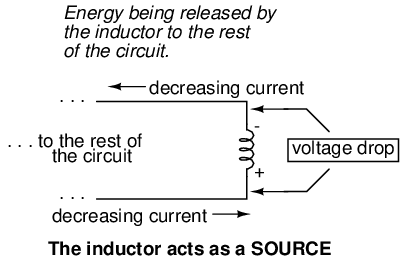
Conversely, when the current through the inductor is decreased, it drops a voltage aiding the direction of electron flow, acting as a power source. In this condition the inductor is said to be discharging, because its store of energy is decreasing as it releases energy from its magnetic field to the rest of the circuit. Note the polarity of the voltage with regard to the direction of current.
If a source of electric power is suddenly applied to an unmagnetized inductor, the inductor will initially resist the flow of electrons by dropping the full voltage of the source. As current begins to increase, a stronger and stronger magnetic field will be created, absorbing energy from the source. Eventually the current reaches a maximum level, and stops increasing. At this point, the inductor stops absorbing energy from the source, and is dropping minimum voltage across its leads, while the current remains at a maximum level. As an inductor stores more energy, its current level increases, while its voltage drop decreases. Note that this is precisely the opposite of capacitor behavior, where the storage of energy results in an increased voltage across the component! Whereas capacitors store their energy charge by maintaining a static voltage, inductors maintain their energy "charge" by maintaining a steady current through the coil.
The type of material the wire is coiled around greatly impacts the strength of the magnetic field flux (and therefore the amount of stored energy) generated for any given amount of current through the coil. Coil cores made of ferromagnetic materials (such as soft iron) will encourage stronger field fluxes to develop with a given field force than nonmagnetic substances such as aluminum or air.
The measure of an inductor's ability to store energy for a given amount of current flow is called inductance. Not surprisingly, inductance is also a measure of the intensity of opposition to changes in current (exactly how much self-induced voltage will be produced for a given rate of change of current). Inductance is symbolically denoted with a capital "L," and is measured in the unit of the Henry, abbreviated as "H."
An obsolete name for an inductor is choke, so called for its common usage to block ("choke") high-frequency AC signals in radio circuits. Another name for an inductor, still used in modern times, is reactor, especially when used in large power applications. Both of these names will make more sense after you've studied alternating current (AC) circuit theory, and especially a principle known as inductive reactance.
Inductors do not have a stable "resistance" as conductors do. However, there is a definite mathematical relationship between voltage and current for an inductor, as follows:

You should recognize the form of this equation from the capacitor chapter. It relates one variable (in this case, inductor voltage drop) to a rate of change of another variable (in this case, inductor current). Both voltage (v) and rate of current change (di/dt) are instantaneous: that is, in relation to a specific point in time, thus the lower-case letters "v" and "i". As with the capacitor formula, it is convention to express instantaneous voltage as v rather than e, but using the latter designation would not be wrong. Current rate-of-change (di/dt) is expressed in units of amps per second, a positive number representing an increase and a negative number representing a decrease.
Like a capacitor, an inductor's behavior is rooted in the variable of time. Aside from any resistance intrinsic to an inductor's wire coil (which we will assume is zero for the sake of this section), the voltage dropped across the terminals of an inductor is purely related to how quickly its current changes over time.
Suppose we were to connect a perfect inductor (one having zero ohms of wire resistance) to a circuit where we could vary the amount of current through it with a potentiometer connected as a variable resistor:
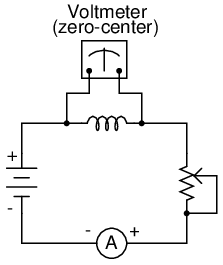
If the potentiometer mechanism remains in a single position (wiper is stationary), the series-connected ammeter will register a constant (unchanging) current, and the voltmeter connected across the inductor will register 0 volts. In this scenario, the instantaneous rate of current change (di/dt) is equal to zero, because the current is stable. The equation tells us that with 0 amps per second change for a di/dt, there must be zero instantaneous voltage (v) across the inductor. From a physical perspective, with no current change, there will be a steady magnetic field generated by the inductor. With no change in magnetic flux (dΦ/dt = 0 Webers per second), there will be no voltage dropped across the length of the coil due to induction.
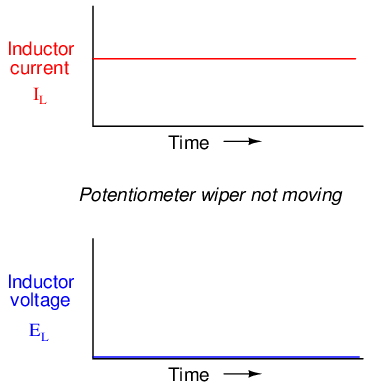
If we move the potentiometer wiper slowly in the "up" direction, its resistance from end to end will slowly decrease. This has the effect of increasing current in the circuit, so the ammeter indication should be increasing at a slow rate:

Assuming that the potentiometer wiper is being moved such that the rate of current increase through the inductor is steady, the di/dt term of the formula will be a fixed value. This fixed value, multiplied by the inductor's inductance in Henrys (also fixed), results in a fixed voltage of some magnitude. From a physical perspective, the gradual increase in current results in a magnetic field that is likewise increasing. This gradual increase in magnetic flux causes a voltage to be induced in the coil as expressed by Michael Faraday's induction equation e = N(dΦ/dt). This self-induced voltage across the coil, as a result of a gradual change in current magnitude through the coil, happens to be of a polarity that attempts to oppose the change in current. In other words, the induced voltage polarity resulting from an increase in current will be oriented in such a way as to push against the direction of current, to try to keep the current at its former magnitude. This phenomenon exhibits a more general principle of physics known as Lenz's Law, which states that an induced effect will always be opposed to the cause producing it.
In this scenario, the inductor will be acting as a load, with the negative side of the induced voltage on the end where electrons are entering, and the positive side of the induced voltage on the end where electrons are exiting.
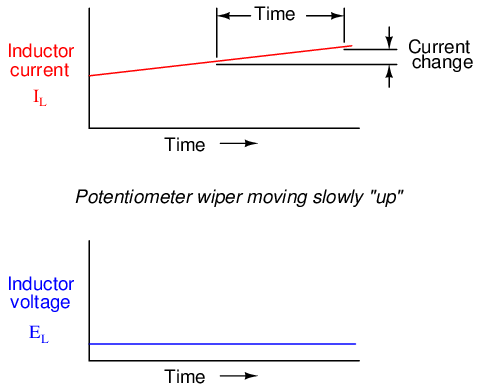
Changing the rate of current increase through the inductor by moving the potentiometer wiper "up" at different speeds results in different amounts of voltage being dropped across the inductor, all with the same polarity (opposing the increase in current):
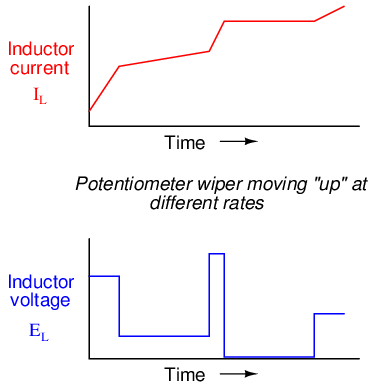
Here again we see the derivative function of calculus exhibited in the behavior of an inductor. In calculus terms, we would say that the induced voltage across the inductor is the derivative of the current through the inductor: that is, proportional to the current's rate-of-change with respect to time.
Reversing the direction of wiper motion on the potentiometer (going "down" rather than "up") will result in its end-to-end resistance increasing. This will result in circuit current decreasing (a negative figure for di/dt). The inductor, always opposing any change in current, will produce a voltage drop opposed to the direction of change:

How much voltage the inductor will produce depends, of course, on how rapidly the current through it is decreased. As described by Lenz's Law, the induced voltage will be opposed to the change in current. With a decreasing current, the voltage polarity will be oriented so as to try to keep the current at its former magnitude. In this scenario, the inductor will be acting as a source, with the negative side of the induced voltage on the end where electrons are exiting, and the positive side of the induced voltage on the end where electrons are entering. The more rapidly current is decreased, the more voltage will be produced by the inductor, in its release of stored energy to try to keep current constant.
Again, the amount of voltage across a perfect inductor is directly proportional to the rate of current change through it. The only difference between the effects of a decreasing current and an increasing current is the polarity of the induced voltage. For the same rate of current change over time, either increasing or decreasing, the voltage magnitude (volts) will be the same. For example, a di/dt of -2 amps per second will produce the same amount of induced voltage drop across an inductor as a di/dt of +2 amps per second, just in the opposite polarity.
If current through an inductor is forced to change very rapidly, very high voltages will be produced. Consider the following circuit:

In this circuit, a lamp is connected across the terminals of an inductor. A switch is used to control current in the circuit, and power is supplied by a 6 volt battery. When the switch is closed, the inductor will briefly oppose the change in current from zero to some magnitude, but will drop only a small amount of voltage. It takes about 70 volts to ionize the neon gas inside a neon bulb like this, so the bulb cannot be lit on the 6 volts produced by the battery, or the low voltage momentarily dropped by the inductor when the switch is closed:
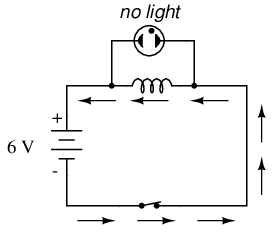
When the switch is opened, however, it suddenly introduces an extremely high resistance into the circuit (the resistance of the air gap between the contacts). This sudden introduction of high resistance into the circuit causes the circuit current to decrease almost instantly. Mathematically, the di/dt term will be a very large negative number. Such a rapid change of current (from some magnitude to zero in very little time) will induce a very high voltage across the inductor, oriented with negative on the left and positive on the right, in an effort to oppose this decrease in current. The voltage produced is usually more than enough to light the neon lamp, if only for a brief moment until the current decays to zero:

For maximum effect, the inductor should be sized as large as possible (at least 1 Henry of inductance).
There are four basic factors of inductor construction determining the amount of inductance created. These factors all dictate inductance by affecting how much magnetic field flux will develop for a given amount of magnetic field force (current through the inductor's wire coil):
NUMBER OF WIRE WRAPS, OR "TURNS" IN THE COIL: All other factors being equal, a greater number of turns of wire in the coil results in greater inductance; fewer turns of wire in the coil results in less inductance.
Explanation: More turns of wire means that the coil will generate a greater amount of magnetic field force (measured in amp-turns!), for a given amount of coil current.
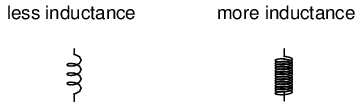
COIL AREA: All other factors being equal, greater coil area (as measured looking lengthwise through the coil, at the cross-section of the core) results in greater inductance; less coil area results in less inductance.
Explanation: Greater coil area presents less opposition to the formation of magnetic field flux, for a given amount of field force (amp-turns).
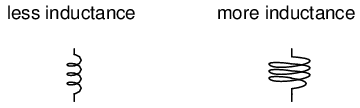
COIL LENGTH: All other factors being equal, the longer the coil's length, the less inductance; the shorter the coil's length, the greater the inductance.
Explanation: A longer path for the magnetic field flux to take results in more opposition to the formation of that flux for any given amount of field force (amp-turns).
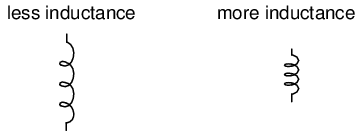
CORE MATERIAL: All other factors being equal, the greater the magnetic permeability of the core which the coil is wrapped around, the greater the inductance; the less the permeability of the core, the less the inductance.
Explanation: A core material with greater magnetic permeability results in greater magnetic field flux for any given amount of field force (amp-turns).

An approximation of inductance for any coil of wire can be found with this formula:
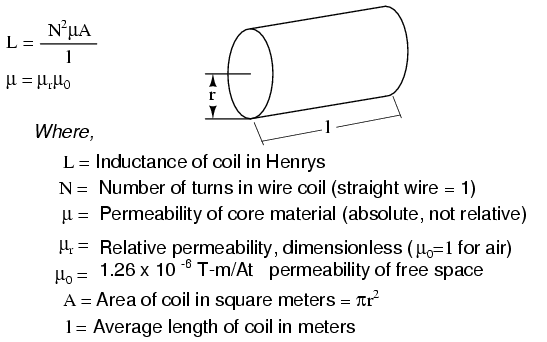
It must be understood that this formula yields approximate figures only. One reason for this is the fact that permeability changes as the field intensity varies (remember the nonlinear "B/H" curves for different materials). Obviously, if permeability (µ) in the equation is unstable, then the inductance (L) will also be unstable to some degree as the current through the coil changes in magnitude. If the hysteresis of the core material is significant, this will also have strange effects on the inductance of the coil. Inductor designers try to minimize these effects by designing the core in such a way that its flux density never approaches saturation levels, and so the inductor operates in a more linear portion of the B/H curve.
If an inductor is designed so that any one of these factors may be varied at will, its inductance will correspondingly vary. Variable inductors are usually made by providing a way to vary the number of wire turns in use at any given time, or by varying the core material (a sliding core that can be moved in and out of the coil). An example of the former design is shown in this photograph:

This unit uses sliding copper contacts to tap into the coil at different points along its length. The unit shown happens to be an air-core inductor used in early radio work.
A fixed-value inductor is shown in the next photograph, another antique air-core unit built for radios. The connection terminals can be seen at the bottom, as well as the few turns of relatively thick wire:

Here is another inductor (of greater inductance value), also intended for radio applications. Its wire coil is wound around a white ceramic tube for greater rigidity:

Inductors can also be made very small for printed circuit board applications. Closely examine the following photograph and see if you can identify two inductors near each other:

The two inductors on this circuit board are labeled L1 and L2, and they are located to the right-center of the board. Two nearby components are R3 (a resistor) and C16 (a capacitor). These inductors are called "toroidal" because their wire coils are wound around donut-shaped ("torus") cores.
Like resistors and capacitors, inductors can be packaged as "surface mount devices" as well. The following photograph shows just how small an inductor can be when packaged as such:

A pair of inductors can be seen on this circuit board, to the right and center, appearing as small black chips with the number "100" printed on both. The upper inductor's label can be seen printed on the green circuit board as L5. Of course these inductors are very small in inductance value, but it demonstrates just how tiny they can be manufactured to meet certain circuit design needs.
When inductors are connected in series, the total inductance is the sum of the individual inductors' inductances. To understand why this is so, consider the following: the definitive measure of inductance is the amount of voltage dropped across an inductor for a given rate of current change through it. If inductors are connected together in series (thus sharing the same current, and seeing the same rate of change in current), then the total voltage dropped as the result of a change in current will be additive with each inductor, creating a greater total voltage than either of the individual inductors alone. Greater voltage for the same rate of change in current means greater inductance.
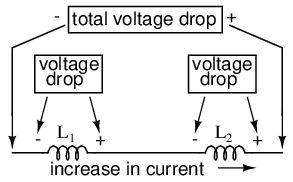
Thus, the total inductance for series inductors is more than any one of the individual inductors' inductances. The formula for calculating the series total inductance is the same form as for calculating series resistances:
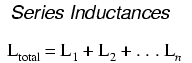
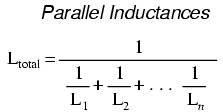
When inductors are connected in parallel, the total inductance is less than any one of the parallel inductors' inductances. Again, remember that the definitive measure of inductance is the amount of voltage dropped across an inductor for a given rate of current change through it. Since the current through each parallel inductor will be a fraction of the total current, and the voltage across each parallel inductor will be equal, a change in total current will result in less voltage dropped across the parallel array than for any one of the inductors considered separately. In other words, there will be less voltage dropped across parallel inductors for a given rate of change in current than for any of those inductors considered separately, because total current divides among parallel branches. Less voltage for the same rate of change in current means less inductance.
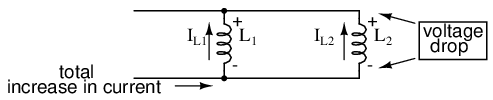
Thus, the total inductance is less than any one of the individual inductors' inductances. The formula for calculating the parallel total inductance is the same form as for calculating parallel resistances:
Inductors, like all electrical components, have limitations which must be respected for the sake of reliability and proper circuit operation.
Rated current: Since inductors are constructed of coiled wire, and any wire will be limited in its current-carrying capacity by its resistance and ability to dissipate heat, you must pay attention to the maximum current allowed through an inductor.
Equivalent circuit: Since inductor wire has some resistance, and circuit design constraints typically demand the inductor be built to the smallest possible dimensions, there is no such thing as a "perfect" inductor. Inductor coil wire usually presents a substantial amount of series resistance, and the close spacing of wire from one coil turn to another (separated by insulation) may present measurable amounts of stray capacitance to interact with its purely inductive characteristics. Unlike capacitors, which are relatively easy to manufacture with negligible stray effects, inductors are difficult to find in "pure" form. In certain applications, these undesirable characteristics may present significant engineering problems.
Inductor size: Inductors tend to be much larger, physically, than capacitors are for storing equivalent amounts of energy. This is especially true considering the recent advances in electrolytic capacitor technology, allowing incredibly large capacitance values to be packed into a small package. If a circuit designer needs to store a large amount of energy in a small volume and has the freedom to choose either capacitors or inductors for the task, he or she will most likely choose a capacitor. A notable exception to this rule is in applications requiring huge amounts of either capacitance or inductance to store electrical energy: inductors made of superconducting wire (zero resistance) are more practical to build and safely operate than capacitors of equivalent value, and are probably smaller too.
Interference: Inductors may affect nearby components on a circuit board with their magnetic fields, which can extend significant distances beyond the inductor. This is especially true if there are other inductors nearby on the circuit board. If the magnetic fields of two or more inductors are able to "link" with each others' turns of wire, there will be mutual inductance present in the circuit as well as self-inductance, which could very well cause unwanted effects. This is another reason why circuit designers tend to choose capacitors over inductors to perform similar tasks: capacitors inherently contain their respective electric fields neatly within the component package and therefore do not typically generate any "mutual" effects with other components.
Contributors to this chapter are listed in chronological order of their contributions, from most recent to first. See Appendix 2 (Contributor List) for dates and contact information.
Jason Starck (June 2000): HTML document formatting, which led to a much better-looking second edition.
Lessons In Electric Circuits copyright (C) 2000-2023 Tony R. Kuphaldt, under the terms and conditions of the CC BY License.


