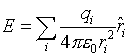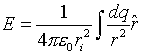Coulomb's Law and the Definition of Electric Field
Coulomb's Law Revisited
Our study of electrostatics began with Coulomb's law:
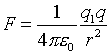
where r
is the distance between charges
q1 and q. We considered F to be the
force between the charges, and realized that, by Newton's third
law, the force on charge q1 was equal and opposite
to the force on charge q. F here is a scalar; it is the
magnitude of the force.
All forces are vectors, of course, and the electric force is no
exception. Our scalar equation does not seem to assign a direction to
the force, but we can do that by remembering that opposite charges
attract, and like charges repel.
When would you calculate the force to be negative?
Physically, what does this mean?
Definition of Electric Field
Now let's consider the vector
F to be the
force
on q due to
q1. We change the
equation slightly:
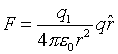
where 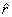 is a unit vector pointing
from q1 to q2. We define the
quantity
is a unit vector pointing
from q1 to q2. We define the
quantity

to be the electric field due to q1 and can now
write F = qE.
If there are several charges, then to find the force on charge
q, we add together (as vectors!) the forces produced by all the
other charges:

where ri is the distance from
qi to q. Again we can write this as
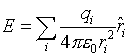
where the sum is a vector sum.
What if we don't have a bunch of discrete charges
qi, but instead have a continuous distribution of
charge? We can break up the source distribution into many small pieces
of charge, and add up all their contributions to the electric
field. In the language of calculus, we are integrating:
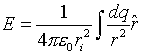
where r is the distance from the piece dq to the point
where the field is measured.
Copyright
1998-1999
Rensselaer Polytechnic Institute. All Rights Reserved.
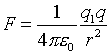
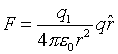
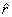 is a unit vector pointing
from q1 to q2. We define the
quantity
is a unit vector pointing
from q1 to q2. We define the
quantity