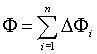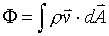Flux through a Curved Surface
The expression for the flux in equation (2) was obtained
for a flat surface. What is the expression for
when the surface is curved? See the figure
below.
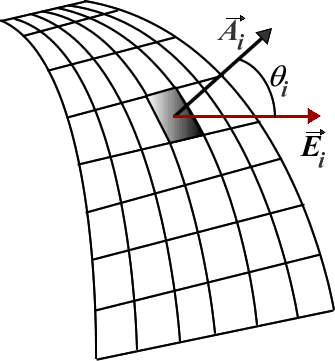 For a curved surface such as the one shown above, the area vector at
each point, in general, differs in both direction and magnitude from
the area vectors at other points. Also, the flow (of water, etc.)
occurs in all different directions and rates. We can then divide the
curved surface into n small segments, so small that each
segment can be viewed as being flat. At the ith
segment, where i is an integer from 1 to n, the area
vector is
For a curved surface such as the one shown above, the area vector at
each point, in general, differs in both direction and magnitude from
the area vectors at other points. Also, the flow (of water, etc.)
occurs in all different directions and rates. We can then divide the
curved surface into n small segments, so small that each
segment can be viewed as being flat. At the ith
segment, where i is an integer from 1 to n, the area
vector is 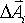 and the water flow
is specified by
and the water flow
is specified by  . Then, by
applying equation (2), the small flux
. Then, by
applying equation (2), the small flux
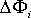 through the
ith segment is
through the
ith segment is 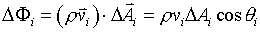
where 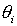 is the angle between the vectors
is the angle between the vectors 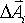 and
and  .
.
The total flux through the curved surface can be obtained by summing
all the 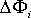 's from i=1 to
i=n.
's from i=1 to
i=n.
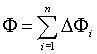
(Remember, i is an integer.)
In the limiting case,

we
obtain
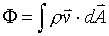
|
(3) |
Notice that this is an area integral. In general, evaluating this
integral will be rather complicated, but in this module we will use it
only in cases of simple geometry.
Once you're ready, go on to our discussion of flux through a Gaussian surface.
Copyright
1998-1999
Rensselaer Polytechnic Institute. All Rights Reserved.


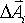 and the water flow
is specified by
and the water flow
is specified by  . Then, by
applying equation (2), the small flux
. Then, by
applying equation (2), the small flux
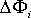 through the
ith segment is
through the
ith segment is 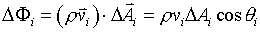
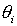
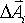 and
and  .
.
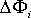 's from i=1 to
i=n.
's from i=1 to
i=n.