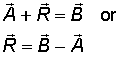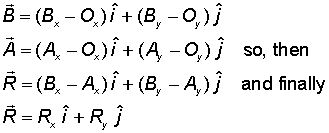Position Vectors
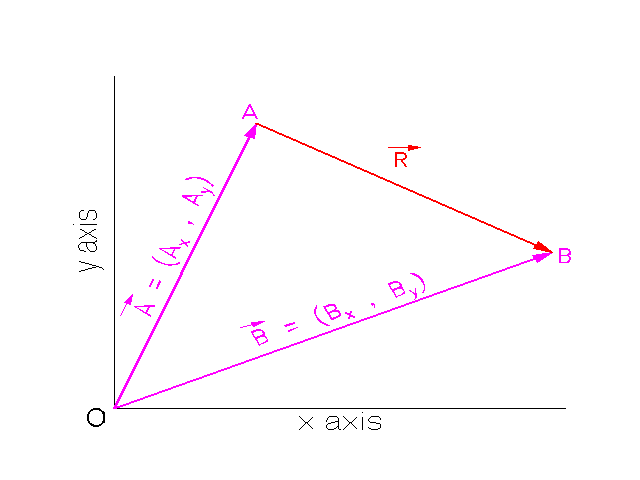
Take a look at the figure below.
Position vectors are vectors that connect two points in space. The figure above shows three position vectors. Vector A describes for us the distance and direction of point A from the origin, O. Vector B shows the position of point B from the origin, O. Vector R shows the direction and distance of point B from point A.To find the vector R notice, from the figure, that
Taking this farther, and using the coordinates of each point, and the unit vectors in the x- and the y-direction, we get
An alternate notation that describes the very same concepts:
A position vector connecting any two points in space can be found by subtracting the coordinates of the tail point from the coordinates of the head point. Written in unit vector notation (for the case above): The magnitude of a position vector is a distance in space and has units of length. Thus the length of a position vector can be found from the Pythagorean Theorem as follows (using notation for this case):
Unit vector notation is explained in greater detail later in the Bicycle Module.
Copyright © 1998 Rensselaer Polytechnic Institute. All Rights Reserved.