Vector Dot Product
Take a look at the figures below.
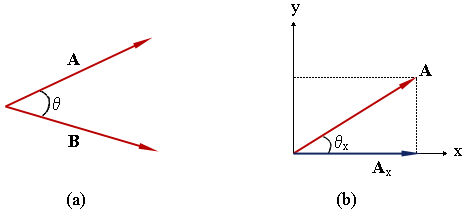
Figure(a) above shows two vectors A and B separated by an angle
. Figure (b) shows a single vector, A
and its component int he x-direction, Ax.
The dot product (also called the scalar product or inner product) of
two intersecting vectors is defined as the product of the magnitudes of the
two vectors and the the cosine of the angle between them. Thus for the figure
above:
If the vectors are given in vector component form, the dot product is computed
on a term by term basis which for (a) above reduces to:
One useful application of the dot product is to find the component of a vector
in a particular direction. This is sometimes called a projection and is computed
by taking the dot product of the vector with a unit vector in the desired
direction. This method also will yield Cartesian components of a vector as seen
in (b), i.e.,
Another application of the dot product allows one to find the angle between two
vectors. Re-arranging the definition of the dot product and solving for the desired
angle yields,
Copyright © 1998 Rensselaer Polytechnic Institute. All Rights Reserved.