Vector Components and Resultants
Take a look at the figure below.
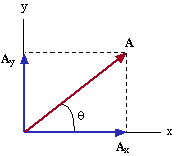
The figure above shows the vector A and its Cartesian component vectors Ax and Ay along the x- and y-axis, respectively. Ax and Ay are components of A since they will vectorially add to produce A according to the parallelogram rule. While there are an infinite number of vector combinations that could add up to A, the most useful components are perpendicular to each other and lie in the Cartesian directions (x and y).

The figure above shows the vector A and its Cartesian component vectors Ax and Ay along the x- and y-axis, respectively. Ax and Ay are components of A since they will vectorially add to produce A according to the parallelogram rule. While there are an infinite number of vector combinations that could add up to A, the most useful components are perpendicular to each other and lie in the Cartesian directions (x and y).
The rectangular scalar components of a vector are related to the
magnitude and the angle of inclination of the resultant vector as follows.
Conversely, the magnitude of the resultant vector and the angle of inclination can be related to the component vectors as follows.
A vector can be written in terms of its components through the use of unit vectors. While a full discussion of unit vectors can be found later in the module, for now realize that the vectors i and j (and k in 3-D) represent vectors along the x and y (and z) axes which have length of 1 and are unitless. The vector is represented as follows:
It should be noted that when letters are used to denote a vector they are emphasized in bold (e.g. A.). When the letter has normal emphasis, it denotes the scalar magnitude of the vector (e.g. A).
Conversely, the magnitude of the resultant vector and the angle of inclination can be related to the component vectors as follows.
A vector can be written in terms of its components through the use of unit vectors. While a full discussion of unit vectors can be found later in the module, for now realize that the vectors i and j (and k in 3-D) represent vectors along the x and y (and z) axes which have length of 1 and are unitless. The vector is represented as follows:
Copyright © 1998 Rensselaer Polytechnic Institute. All Rights Reserved.