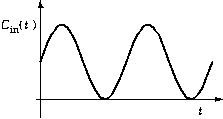
It is of course represented by some type of a sin function. We write the general sinusoidal function in this module as
A sinusoidal input function varies periodically:

It is of course represented by some type of a sin function. We write
the general sinusoidal function in this module as

where a is the normalized amplitude, T is the period (i.e., the function repeats in time period T), and Ci is the average input concentration. (Note that at times 0, T, 2T, etc., the sinusoidal function is zero, so the actual input concentration is the average concentration Ci. When the sin function reaches its maximum, then the input is Ci(1 + a), and at the sin function's minimum, we have concentration Ci(1 - a).)
Note that in our model, a is not the actual amplitude of the sinusoidal function, but is a normalized amplitude and is always between zero and one. By examining the equation, we see that the actual amplitude of the sin function is Ci a. The value a must stay less than one, or else the concentration in the input would be negative, which of course is impossible. At zero, there is no sinusoidal component.
We use a sinusoidal input function to represent situations in which the input concentration of contaminant varies periodically. While it may seem unusual, there are actually many situations which this models well. For example, seasonal variations may affect contaminant levels, and a plant dumping waste may produce less output at night than during the day when it operates.
Of course, it may be that the variations are not very significant in comparison to the average concentration or they may be insignificant over a large time frame. Under some situations, it might be as effective to use a step input function instead. The significant points are that:
To return to the page you came from, press the Back button on your browser.