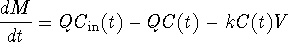
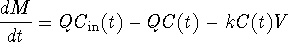
We are concerned with monitoring the change in mass with respect to time of a particular substance within our control volume. However, the total M is simply the concentration times the volume (assumed constant), or M(t) = V C(t):
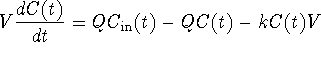
Then we divide by V on both sides to get the following:
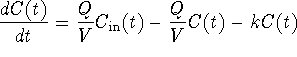
Now if we divided V (a volume) by Q (a flow rate), we
would get units of time. In fact, the volume divided by a flow rate
would give how long it would take to either fill the volume if no flow
were exiting, or flush the volume if no flow were leaving. We can
also think of this time as on average how long an infinitesimal
particle sits in our control volume from the time it enters to the
time it exits. This is commonly referred to as the residence
time and denoted by the symbol ![]() .
Thus we now have the following:
.
Thus we now have the following:
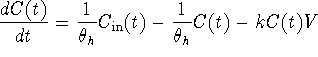
This is the form we will use. It is relatively simple, versatile, and reasonably accurate, and based on our four assumptions. You should now be ready to return to the beginning and understand the equations used in this module.
 Go back to
"Lake Pollution Module Main Page".
Go back to
"Lake Pollution Module Main Page".
![]()
![]()
![]()
Up: Beginning
Previous: A4: Well-Mixed