Suppose a particle moves along a curve so at time t its position is r(t) = (f(t), g(t))). Then:
- the velocity vector is the first derivative: r'(t) = (f'(t),g'(t)).
- the speed is the magnitude of the velocity:
- the acceleration of the particle is the second derivative: r''(t) = (f''(t), g''(t)).
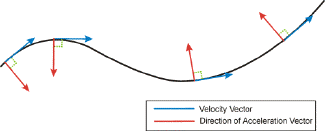
Notice that the speed might be constant, even though the velocity vector is changing direction. Thus the particle can have an acceleration even when the speed is constant.
If the particle now moves along the curve in such a way that the speed is constant and always equal to 1, then the length of the acceleration vector at time t is also the curvature of the curve at the point .
Go to the discover page to see the acceleration along a path.
Non-constant speed


The figures above show some acceleration vectors on a curve when speed is not constant. Study the figures, then go to the practice page.
Applications of Acceleration in Design
If you drive along a curved road at a constant speed, and the curve has a high curvature, there is a non-constant acceleration vector and you can feel the changing force. Note that curvature can also be defined in three dimensions, so that this has important applications for designers of paths for highways, railroad tracks, and roller coasters. For example, for high-speed trains it is necessary to make the tracks very straight, or almost zero curvature, for otherwise the force from acceleration would knock the train off the track.