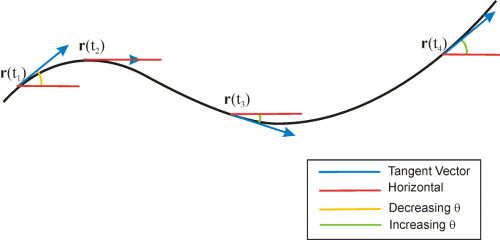

Definitions:
- The tangent angle q is the angle that the tangent vector makes with the horizontal vector <1,0> (measured counterclockwise as shown).
- The arc length is the length along the curve between two points.
- A curve is parameterized by arc length if the arc length from r(a) to r(s) is s for all s in [a,b].
|
We can re-parameterize a curve so that it is parameterized by arc length, and then the tangent vector at a point r(s) on a curve of unit length. This means that for a curve parameterized by arc length is also a function of s. |

|

Definitions:
- The signed curvature is the derivative of the tangent angle with respect to arc length.
- The curvature is the absolute value of the signed curvature.
Go to the discover page to see the a tangent angle in action.
Turning Angle
Definition: The turning angle of a curve from s1 to s2 is Answer some questions about the tangent and turning angles on the practice page. |
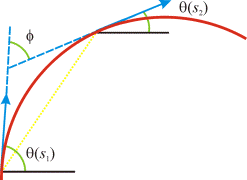
|
Tangent, Starting Point, and Curvature: All you need!
A famous theorem states that if the signed curvature is known as a function of arc length and the starting point and starting tangent direction are given, then the curve is completely determined. This is not so surprising, given that the curvature determines the turning angle at all points along the curve as indicated in the formula in the preceding paragraph.