drag coefficients
Relationship of k and Cd
Regardless of the kind of object in motion or the fluid through which it moves, the drag force is
usually represented in terms of a dimensionless drag coefficient using the equation (e.g. see
reference [4])
| where, |
= drag force on the object, (N)
= drag coefficient, dimensionless
= a characteristic area for the object, (m2)
= fluid density, (kg/m3)
= relative velocity between the object and the fluid, (m/s) |
We may ask how the drag force coefficient
k is related to the drag coefficient,
Cd. In the
section on
"Falling in a Fluid" we
introduced the following equation for
FdSince vf and vr are the same in this context
The equation of motion in terms of Cd is, using eqn. (3.2),
The characteristic area, A, is arbitrarily selected for a particular shape of object. For a sphere
where
d is the diameter of the sphere.
A is the largest area seen by the fluid passing over the object.
In the formulation of the differential equation (3.1), k (therefore also Cd) was assumed to be constant. In reality these coefficients are not constant when the drag force is considered over a wide range of values of the velocity vf
or Reynolds number R (defined below). Data for the drag coefficient for a sphere (the standard drag
curve for a sphere) is shown below. Similar plots exist for other objects
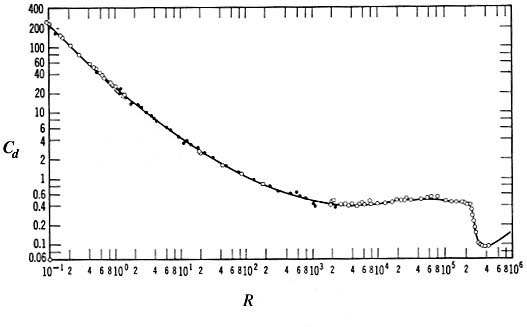
Note in the plot that
Cd is a function of another dimensionless group, , called the Reynolds number
where = viscosity of the fluid, (Ns/m
2)
We can see from the Cd vs. R plot above that Cd = kvf2 with k constant applies reasonably
well for R values between 7.5x102 and 2x105. For values of R below 7.5x102
the value of Cd is higher than in the constant Cd region and varies with velocity.
For the various R intervals
These equations are valid only for solid smooth spheres and apply for R values from 0 to 2x105.
Cd is inversely proportional to vf for small values of vf. Following a transition region, Cd becomes essentially constant. The integration of eqn. (FL 3.4) is more
complicated as a result since Cd is a function of vf which varies as the diver falls.
Copyright © 1998 Rensselaer Polytechnic Institute. All Rights Reserved.
