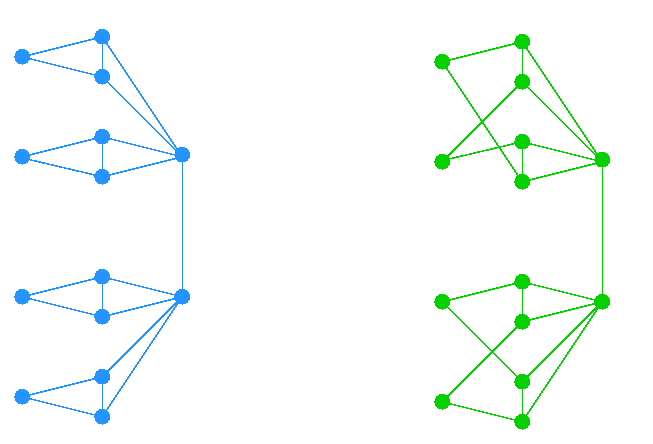
However, for many graphs, such a reduction is of little help, or even no help at all. Regular graphs are a prime example. Furthermore, even if we discover that two given graphs satisfy Proposition 3, we still don't know whether these graphs are isomorphic.

10-1) Show that these two graphs satisfy Proposition 3 and
that they are non isomorphic.