If is a bijective isomorphic mapping, then must equal by the definition of a bijection. Proving is equally easy.
Another useful graph
invariant is the sequence of degrees of the vertices. Grouping
vertices by ascending degree is a straightforward partitioning method.
For any vertex , ??? the vertices adjacent to v are mapped onto the vertices in that are adjacent to . Thus, . More importantly, the degree of v is equal to the degree of .
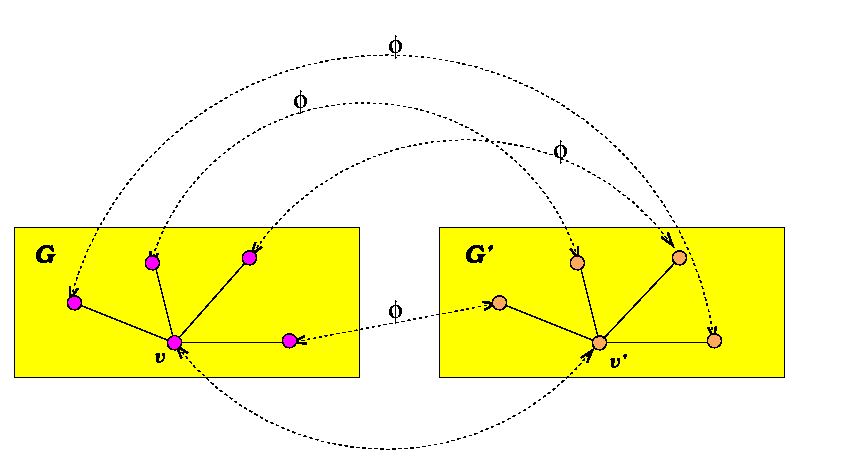
Proposition 1 is a very simple statement among those that are used by a
method called the refining technique.
Other statements of the same kind are given in the
three collaborative problems.