Theoretical Consideration
How different (harder) is the colored graph isomorphism problem from
the uncolored graph isomorphism problem?
Clearly, the uncolored graph isomorphism problem is a special case of the colored
one: if
and
are two uncolored graphs, then we can always assign to every vertex and every
edge the same color which transfers the pair of graphs into a pair of color
graphs. This does not change the essence of the problem since the color
is identical to all edges and vertices of both graphs.
Surprisingly, the colored graph isomorphism problem can be reduced to the uncolored
graph isomorphism problem by a suitable transformation of the input colored
graphs into corresponding uncolored graphs. First, notice that if the
colors used for one graphs are different from that of the other graphs, then
the graphs are non-isomorphic. Furthermore, we can assume that the colors
used for vertices are different from the colors used for edges.
We can always start solving the isomorphism problem by checking if the list
of colors used for one graph is identical to that for the other. The transformation
described on this page is executed after this checking is done. Then,
we transform every labeled graph into an unlabeled graph and see if the resulting
uncolored graphs are isomorphic. Then and only then are the initial colored
graphs isomorphic.
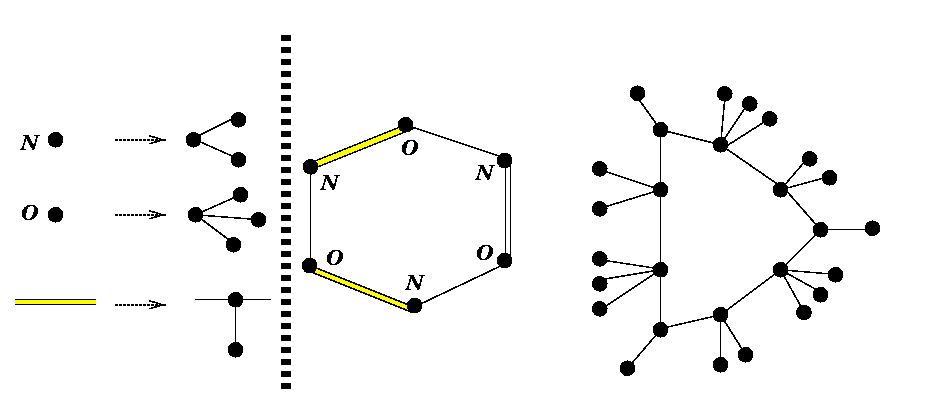
In the left part of the figure, it is shown that the vertex labeled with N
(resp. O) is replaced with an unlabeled vertex adjacent to
two (resp. three) new vertices; the new vertices are of degree one each.
Every edge showing a double link is replaced with a new vertex adjacent to the
vertices that were connected by the edge. Every vertex replacing a double
link is made adjacent to an additional new vertex of degree one.
Copyright
2000
Rensselaer Polytechnic Institute. All Rights Reserved.

