Answer to Problem 19
We will prove it by induction on  , the (finite) number of vertices.
, the (finite) number of vertices.
(Base case): If 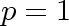 ,
then the number of edges,
,
then the number of edges,  , is
, is  , and the statement holds.
, and the statement holds.
(Inductive step): Let the
statement hold true for any tree with
 vertices,
vertices,
 ,
and let
,
and let 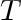 be a tree with
be a tree with  vertices.
vertices.
If the degree of every vertex in 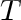 were
were
 ,
then we would be able to construct a cycle as follows:
,
then we would be able to construct a cycle as follows:
-
Start at any vertex
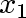 and select a vertex
and select a vertex  adjacent to it.
adjacent to it.
-
Then select a vertex adjacent to
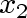 but different from
but different from 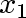 .
.
-
Continue this way by selecting a new vertex which is different from the one selected just before.
(This is possible if the degree of every vertex is
 ).
).
- Since the graph is finite, at some moment we will have to select a vertex which has already been selected more than one step previously. Such a selection creates a cycle, which a tree cannot have.
Now, let  be a vertex of degree 1 in
be a vertex of degree 1 in  . If we remove
. If we remove
 together with the edge incident to it from
together with the edge incident to it from 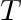 , then the remaining graph
, then the remaining graph
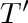 has no cycles and is connected (be sure you are convinced of this before proceeding).
has no cycles and is connected (be sure you are convinced of this before proceeding).
Thus, 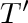 is a tree. By induction, the statement
is correct for
is a tree. By induction, the statement
is correct for 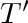 :
:

Equation 7
But,
 and
and
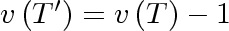 .
.
Therefore,
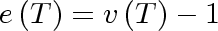 .
.