External Page
Proving that the answer is
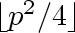 can be done by induction on the number of vertices.
can be done by induction on the number of vertices.
An uncommon feature of the proof is that the
base of the induction consists of two values of
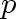 :
:
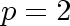 and
and
 .
The corresponding graphs are the complete
.
The corresponding graphs are the complete
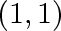 -bipartite
graph and the complete
-bipartite
graph and the complete
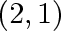 -bipartite
graph:
-bipartite
graph:
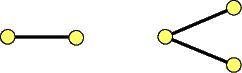
Figure 12:
For both of the above graphs any path of length 2 is an induced subgraph (the first doesn't even have such paths). Under this condition, the graphs have the maximum number of edges among all such graphs with
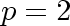 and
and
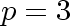 vertices, respectively.
vertices, respectively.
Now, assume that our answer holds true for all graphs with up to
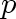 vertices, and let
vertices, and let 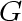 be a graph with
be a graph with
 vertices
which has no triangles. Since
vertices
which has no triangles. Since 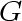 must have
at least one edge, select an arbitrary edge
must have
at least one edge, select an arbitrary edge
 and remove from the graph both
vertices
and remove from the graph both
vertices 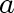 and
and  together with the edges incident to them.
together with the edges incident to them.
The resulting graph
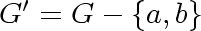 has no triangles; it has
has no triangles; it has 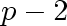 vertices;
thus, inductively, the number of edges in
vertices;
thus, inductively, the number of edges in
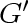 is at most
is at most
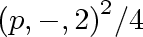 .
.
Now we count the number of edges removed from 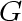 when
when
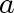 and
and 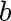 are removed.
Since
are removed.
Since 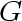 has no triangles, for every vertex in
has no triangles, for every vertex in
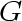 other than
other than 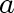 and
and 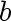 ,
at most one edge adjacent to
,
at most one edge adjacent to 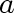 or
or 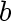 is removed.
Therefore, the number of edges removed is bounded by
is removed.
Therefore, the number of edges removed is bounded by

Equation 2
where one counts the removal of edge
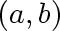 .
.
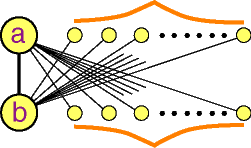
Figure 13:
the vertices adjacent to b are not adjacent to a the vertices adjacent to a are not adjacent to b
We are now in a position to estimate the total number of edges in 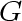 :
:
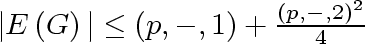
Equation 3
simplifying, we get
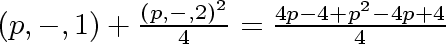
Equation 4
... and simplifying this further, we conclude the proof:
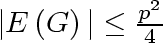
Equation 5