Answer to Problem 32

Equation 25
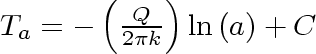
Equation 26
Subtraction gives:
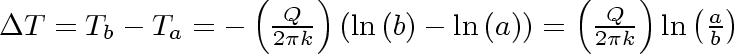
Equation 27
Therefore
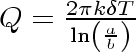
Equation 28
Then
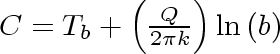
Equation 29
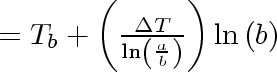
Equation 30
Substitution for
 and
and
 in (4.4) yields
in (4.4) yields
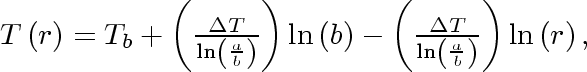
Equation 31

Equation 32
Note that when
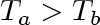 ,
,
 is positive, the heat flow is directed radially
outward. Note further that in this case of radial
conduction through a cylindrical wall, the
temperature distribution is logarithmic.
is positive, the heat flow is directed radially
outward. Note further that in this case of radial
conduction through a cylindrical wall, the
temperature distribution is logarithmic.
A little manipulation yields the result in the symmetric form

Equation 33