Analysis Link 1
Derivation of Partial Differential Equations for Steady State Heat Conduction from Vector Calculus.
Instead of the derivations given for examples 1, 2b, and 3 in Heat Conduction I and equation (3.1) in Section 3 of this module, we can use a more general procedure which involves vector calculus. It will become apparent for the simple problems just mentioned that the vector method is an excessively heavy instrument. But as the problems to be dealt with become more complicated in geometry and the number of directions of heat flow increases, it becomes more advantageous, even necessary, to use the appropriate partial differential equation.
Consider a solid of conductivity k whose interior we denote by V. Suppose T, the temperature in V, has continuous partial derivatives up through the second order.
Suppose further that T is independent of time, that is, we are in a steady state.
a. Partial differential equation when there are no sources or sinks of heat in V.
We will show that at each point of V, T must satisfy the
partial differential equation.
| (L1) |
|
|
|
If k is a constant this governing equation reduces to
| (L2) |
|
Equation (L2) is known as Laplace's equation.
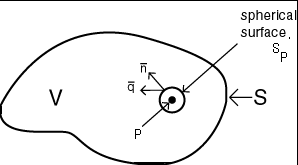
To derive equation (L1), we start by choosing an arbitrary point P in V as shown in Figure 2
Since P is an interior point of V, there exists a spherical surface SP centered at P lying entirely within V. The spherical surface, SP, encloses a volume VP. is not generally perpendicular to SP,as is.
Let Qp(watts) denote the net outflow of heat through SP. Then
| (L3) |
|
|
| where | ||
|
|
the heat flux vector at each point of (W/m2), | |
|
|
|
outward drawn normal to |
|
|
|
component of the heat flux vector in the direction of |
|
|
|
net outflow of heat through |
By Fourier's law
| (L4) |
|
| (L5) |
|
| (L6) |
|
Note that is a vector having magnitude and direction. is a scalar representing the component of in the direction of . Qp is a scalar representing the integral sum of all the heat flux components on the surface SP.
We now use the Divergence Theorem (See Math Link 1) to convert the surface integral into a volume integral. Using equation (L22) in Math Link 1 with , equation (L3) can be written
| (L7) |
|
In the steady state, the net rate of heat outflow, Qp, is constant. Furthermore since no heat is generated or absorbed within VP, then Qp must be zero, so that
| (L8) |
|
Because T has second order partial derivatives that are continuous, the integrand of equation (L8) is continuous enabling us to show that
| (L9) |
|
Suppose that at P,and to be specific assume it is greater than zero. If this is so then there must be a sufficiently small spherical neighborhood of P, SP, contained in V in which
| (L10) |
|
This would make the integral in equation (L8) positive. Since the assumption in equation (L10) has led to a contradiction of equation (L8), we conclude that equation (L9) is correct. Since P is an arbitrarily chosen point in V
| (L11) |
|
and also
| (L12) |
|
Equation (L11) is identical to equation (L1). If k is a constant we obtain equation (L2) (Laplace's equation)
| (L13) |
|
b. Effect of the coordinate system on the scalar equation.
The scalar representations of equations (L9) and (L11) can be written in any coordinate system. For example, Laplace's equation (Equation L2) in Cartesian (x, y, z) and cylindrical (r, , z) coordinates are written
| (L14) |
|
| and | |
| (L15) |
|
| respectively. | |
It is apparent that equation (L11) simplifies to equation (2.1) for steady state conduction in the x - direction and to (2.2) for steady state conduction in the r - direction. When k = k(T), equation (L13) is written.
| (L16) |
|
which simplifies to equation (2.3) for steady state conduction
in the x - direction.
It should be apparent that for simple problems, the vector method is overly
complicated.
c. Heat generation at rate Qgen within V
| (L17) |
|
because the net heat flow leaving the volume V must equal the heat generation inside V. In fact
| (L18) |
|
where Qgen = Q(x,y,z) = local heat generation, W/m3
Rewrite (L18) as
|
|
| (L19) |
|
Equation (3.1) is easily derived from equation (L19)
since for one dimensional steady state conduction in the x direction
when k is a constant. Thus
| (L20) |
|
For radial heat conduction with heat generation and k constant, equation (L19) gives
| (L21) |
|
Copyright © 1998 Rensselaer Polytechnic Institute. All Rights Reserved.