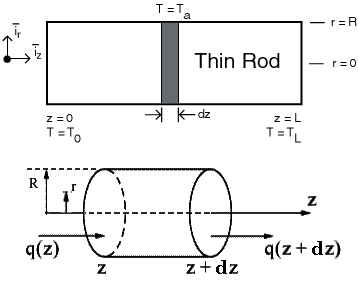
We have assumed previously that the cylindrical surface at r = R was perfectly insulated ( dT/dr = 0 at r = R). Now we will assume instead that there is a heat loss at r = R at any z and represent that loss in terms of a convective heat transfer coefficient so that
| (3.21) |
|
| where | qR(z) = radial heat flux at r = R at a distance z along the rod, W/m2 |
| h = convective heat transfer coefficient, W/m2K | |
| T(z) = temperature in the rod at distance z along the rod, K | |
| Ta = ambient air temperature, K |
One can get sense of the meaning of equation (3.21) by reference to the wind chill effect. We all know how much colder one feels when the wind is blowing.
The reason for this is that instead of losing body heat due just to the difference in temperature between one's body and that of the air passing over that body, the velocity of the air is also a factor.
Thus we see in equation (3.21), the heat loss being proportional to the difference in temperature between the surface of the body and the ambient temperature (T(z) - Ta) and a heat transfer coefficient (h) which is a function of the air velocity and other relevant factors which are discussed in books (or sections in books) on convective heat transfer such as in Incroprera and DeWitt.
Equation (3.21) is often referred to as Newton's law of cooling.
We also assume steady axial heat conduction in the z direction and heat generation due to the electric current passing through it. We also assume that the thermal conductivity of the rod is constant.
Consider the rod (Figure 4)
The heat balance on an element of volume of the cylindrical rod in this problem includes contributions due to heat conduction, heat loss at the periphery of the rod and electrical heat generation. Let us consider each term in the differential equation.
1. Heat conduction in the z direction on an element dz with
To > TL is
| In at z |
|
units: Watts |
| Out at z + dz |
|
|
| Net heat flow out of the element is | ||
| (3.22) |
|
|
| We can relate the temperature derivative at z to that at z + dz by Taylor's theorem. Thus | ||
| (3.23) |
|
|
|
Using equation(3.23) in equation (3.22), we obtain the net heat flow in the z direction as |
||
| (3.24) |
|
units: Watts |
|
2. Heat loss at the periphery of the element in terms
of the convective heat transfer coefficient is represented as follows:
|
||
| (3.25) |
|
|
|
Here we assume that T is constant in the r direction. |
||
|
3. Heat generation due to the electrical current
passing through the rod (ohmic heating) is
|
||
| (3.26) |
|
|
|
where I = current (amps) and e = resistivity (ohms m). |
||
Summing all aforementioned contributions [equations ((3.24)), (3.25) and (3.26)], the heat balance on the element in Figure 4 is
| (3.27) | |||||
| |
+ |
= |
|||
| Out - In by conduction |
Loss at surface of rod |
Heat generation in the rod |
The heat generated in the element must flow out to maintain a steady state.
| The differential equation is finally | ||
|
|
||