Eigenvalues & Eigenvectors
Most texts on linear algebra introduce eigenvalues and eigenvectors in the following analytical way:
If A is a 2 x 2 square matrix, and I is a 2 x 2 identity matrix, then the set of scalars for i=1,2 that satisfy the characteristic equation |A - I| = 0 are called eigenvalues (or characteristic roots) of A. Eigenvalues may be real or complex numbers.
Each eigenvalue will have an eigenvector associated with it. The eigenvector v is the solution to the equation Av = v. (Note: "Eigen" means "proper" in German, so older texts often refer to eigenvectors as proper vectors.)
These equations also have important geometric meanings which are not often discussed. Consider
Av = v, where
A is a matrix,
v is a vector and is a scalar. Geometrically, the real eigenvectors
v of a matrix
A are the subset of all
x vectors in the plane whose direction remains unchanged by the transformation
A (complex eigenvectors do not have this same geometric meaning). That is, the transformed vector
Ax is simply a dilation of the vector
x, where the dilation factor is the absolute value of eigenvalue associated with the eigenvector. If abs() < 1, then
Av is shorter than
v. If abs() > 1, then
Av is longer than
v. The sign of indicates whether
Av and
v are pointed in the same direction ( is positive) or the opposite direction ( is negative).
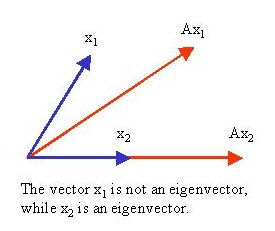
The real eigenvectors of a matrix also form lines. These lines are known as eigendirections.
Copyright
1998-1999
Rensselaer Polytechnic Institute. All Rights Reserved.

