
The mathematical model is obtained by applying laws of nature to the physical model. Our simplifying assumptions lead to a mathematical model consisting of a linear ordinary differential equation with constant coefficients. This model is less realistic, but it retains essential characteristics of the physical system and is much easier to solve and use.
Click here to see the assumptions for our model and the consequences which result from those assumptions.
To develop a mathematical model, first decide what the variables are and choose a coordinate system.
If the independent variable is time t, which of the following are the dependent variables?
What choices of the following should you make in order to specify the coordinate system?
The following clickable diagram represents our choices for the coordinate frame. As you proceed, keep in mind how the choice of the positive direction affects the derivation.
The study of mechanical systems is based on the balance of forces. The applicable law of nature is Newton's Second Law F=ma (which states that the product of the mass m and its acceleration a is equal to the net force F acting on the mass.) To apply Newton's Second Law, you should identify the forces acting on each mass and show them in a Free Body Diagram (FBD).
Click on the question marks in the FBD below to label the forces when the masses have positive displacement and velocity.
 |
 |
 |
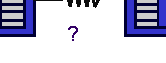 |
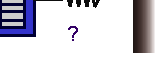 |
The forces acting on the left mass are:
The forces acting on the right mass are:
What do you think is the mathematical expression for the WEIGHT?
Recall that our physical model system has two springs, but our model has only one spring.
What do you think is the mathematical expression for the SPRING FORCE?
What do you think is the mathematical expression for the DAMPING FORCE?
Now you can express Newton's Law mathematically. You need to write F and a in terms of x, t, l, k, m, c, and g.
How can the net force F be written? How can the acceleration a be written? What does Newton's Law give in this case?
The result can be expressed as ![]()
To simplify this Ordinary Differential Equation (ODE), we reduce it to this to the homogeneous ODE. To see how, click DERIVE.
From here on, we will use x instead of ![]() ,
so
,
so
 |
To describe the problem completely, it is necessary to specify the initial state of the system.
How many initial conditions do you need? (What is the order of the differential equation?)
What would be good choices for the initial conditions?
The differential equation along with the initial conditions form the mathematical model for the spring mass system.