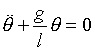
What quantities do you think characterize the motions of oscillating systems such as a pendulum? More specifically, if you wanted to compare the behavior of an actual pendulum and a model pendulum, what quantities would you compare? This section will help you find out.
The mathematical model for the simple pendulum system can be written as
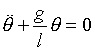
 and
and 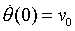
We want to solve this initial value problem. To see what method to use, it helps to classify the differential equation.
What is the general solution of this differential equation?
where
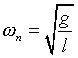
The parameter 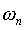 is the natural frequency of
vibration. Using the initial conditions to determine A and
B, we find the solution
is the natural frequency of
vibration. Using the initial conditions to determine A and
B, we find the solution
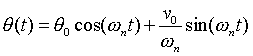 |
A formula that is easier to understand and to visualize is
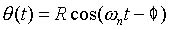
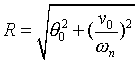 and
and 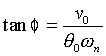 . Click here
to see a derivation of this type of formula.
. Click here
to see a derivation of this type of formula.
According to this formula, the mass undergoes simple harmonic motion
of amplitude R and frequency 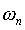 , with phase angle
, with phase angle  . Both the displacement and the velocity are
quantities of interest.
. Both the displacement and the velocity are
quantities of interest.
What is an expression for the velocity in terms of t?
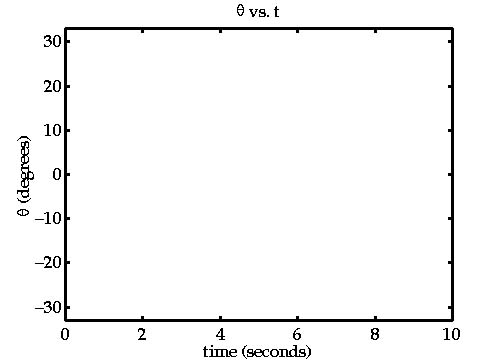
A graph of the angular displacement for typical initial conditions can be seen by Clicking here
The corresponding graph of the angular velocity can be seen by Clicking here
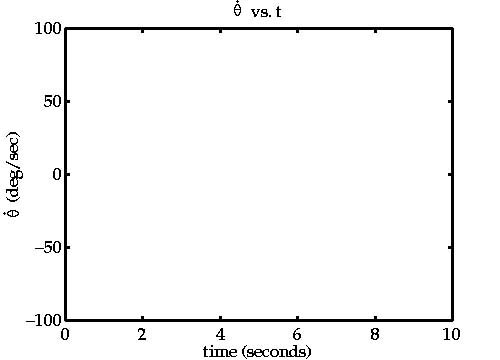
What do you think was the value of 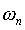 used for these plots?
used for these plots?
Another way of presenting this information is by a parametric plot with t as a parameter, using the displacement as the horizontal coordinate and the velocity as the vertical coordinate. Click here to see this parametric plot.
Does this graph remind you of anything?
How was the equation for the graph derived?
The 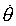 versus
versus 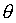 representation is a plot in the Phase
Plane or State Space.
representation is a plot in the Phase
Plane or State Space.
What do the arrows represent?
Why are the arrows pointing in the clockwise direction?(Hint: if the velocity is positive, is the displacement increasing or decreasing?)