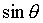 by
by 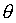 . When is the magnitude of the error caused by
this approximation less than, say, 10% of the magnitude of the
actual function?
. When is the magnitude of the error caused by
this approximation less than, say, 10% of the magnitude of the
actual function?
In our differential equation, we have approximated 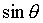 by
by 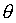 . When is the magnitude of the error caused by
this approximation less than, say, 10% of the magnitude of the
actual function?
. When is the magnitude of the error caused by
this approximation less than, say, 10% of the magnitude of the
actual function?
The actual function is 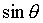 , so 10% of that is
, so 10% of that is  . The absolute error between
. The absolute error between 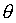 and
and 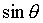 is
is 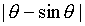 . Thus, the absolute error is less than 10% of
the magnitude of the actual function when
. Thus, the absolute error is less than 10% of
the magnitude of the actual function when
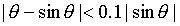
For what values of 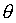 is
is 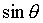 close to
close to 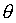 ? To help you, a graph shows
? To help you, a graph shows 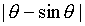 in blue and
in blue and  in green.
in green.

What if you wanted a 5% error? Estimate the valid range of theta
for this case.
We have addressed the issue of how close 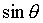 is to
is to 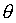 , but not the issue of
how close the solution of the linearized pendulum equation is to
the solution of the nonlinear pendulum equation. We will return
to this more difficult and important issue later in the module.
, but not the issue of
how close the solution of the linearized pendulum equation is to
the solution of the nonlinear pendulum equation. We will return
to this more difficult and important issue later in the module.