 |  |  | |||
n g l e | 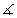 1 1 | Case 1 | Case 2 | Case 3 | |
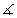 2 2 | Case 4 | Case 5 | Case 6 | ||
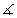 3 3 | Case 7 | Case 8 | Case 9 | ||
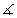 4 4 | Case 10 | Case 11 | Case 12 | ||
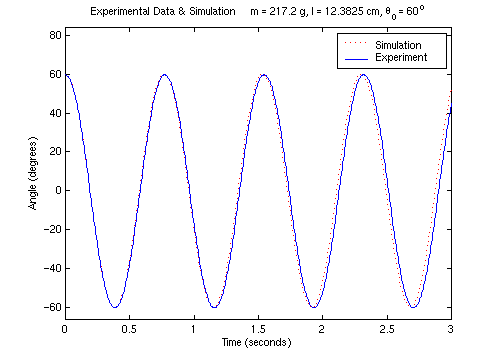

We compare the expected performance of our pendulum model with actual data from several experiments. This comparison will demonstrate the utility of the mathematical model, as well as its limitations.
For what ranges of the
parameters of the system (mass, length of the rod, initial conditions) do you
think that our mathematical model will give accurate predictions?
Here are the experimental data and the simulations for one mass, three different effective lengths, and four different sets of initial conditions. Compare the data and simulations for the undamped nonlinear pendulum.
|
|||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||
Take a look at:
Do you think that the agreement between the predicted frequency and the actual frequency will always be this good?
Examine the following plots to find out:
Overall, our simulations match our data very well. Why do you think that the frequency of the model does not always exactly match the frequency of the data?
If we only considered the first two or three oscillations of the pendulum, would it be noticeable that the frequencies differed? Examine:
Why does the model work better for a few oscillations?
Take a look at various different cases and compare between the short time and the long time plots. What do you observe?
Do you think that if we had data for several minutes, as opposed to 15 seconds, that the agreement with model results for case 8 would break down?
Let's now concentrate data and simulations for large initial angles:
Is the agreement between experimental data and simulations better for small or for large angles? Why?
After comparing the model's predictions for each of the cases illustrated the following is clear:
What is the most reasonable explanation for the decaying amplitude in the experimental data? What additional physical considerations can improve the model?