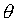 is counterclockwise.
is counterclockwise.To develop a mathematical model first decide what the variables are and choose a coordinate frame. The experimental results presented in the actual dynamic behavior page suggest what choices we should make for the independent and the dependent variables. Let us discuss this issue in more detail.
If the independent variable is time, t, which of the following is the dependent variable?
To fix a coordinate frame, you must choose
What do you think would be good choices? Compare your answer to the correct one.
Since the motion is rotational, we choose a polar coordinate system with the
origin at the point where the rod is attached to the support. The polar axis is
straight down and the positive angular direction 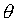 is counterclockwise.
is counterclockwise.
The diagram shows these choices.

A good starting point for the study of this system is Newton's Second Law
What are the forces acting on the mass?
In the diagram, identify the forces by clicking on the arrows.
 |
|
Newton's Second Law is a vector equation. For the pendulum system it is convenient to choose one component in the
positive 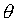 direction (tangent to the arc described by the bob's motion), and one in
the r direction (perpendicular to the arc described by the bob's motion). Since the bob doesn't move in the radial
direction (its r coordinate is the constant l), we can concentrate on the tangential equation
direction (tangent to the arc described by the bob's motion), and one in
the r direction (perpendicular to the arc described by the bob's motion). Since the bob doesn't move in the radial
direction (its r coordinate is the constant l), we can concentrate on the tangential equation
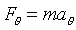
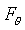 and
and
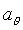 are the theta components of force and acceleration. Notice how our choice of
coordinate systems has simplified this problem.
are the theta components of force and acceleration. Notice how our choice of
coordinate systems has simplified this problem.
To proceed further, you need to rewrite 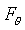 and
and 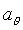 in terms of t,
in terms of t, 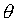 (t), l, T, m, and any necessary
universal constants, such as g.
(t), l, T, m, and any necessary
universal constants, such as g.
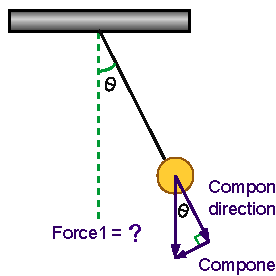
To rewrite 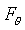 you need to find the theta components of the forces. Draw a picture and do this. When you are ready, compare your answer to the correct one.
you need to find the theta components of the forces. Draw a picture and do this. When you are ready, compare your answer to the correct one.
 |
 |
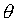 is in the -
is in the -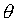 direction so the component in the +
direction so the component in the +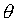 direction is -mg sin
direction is -mg sin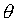 .
.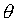 direction is zero.
direction is zero. 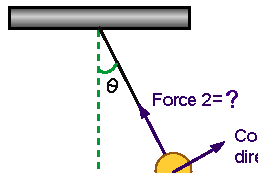 |
 |
 | |
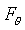 is the sum of the
is the sum of the 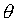 components of gravity and tension.
components of gravity and tension.
What is 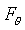 ?
?
What about the components in the radial direction? To investigate further go to collaborate.
Now you need to rewrite 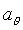 .
.
If the pendulum moves through an angle 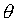 , what is the distance traveled by the bob? (What is the length of its arc?)
, what is the distance traveled by the bob? (What is the length of its arc?)
Given the displacement of the bob, what is its acceleration?
Now put your expressions for 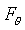 and
and 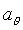 into
into 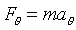 so
so
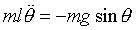
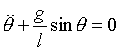
Would this equation be different if we had chosen theta to be positive in the clockwise direction?
What steps on the way would have been different?
This equation for the angular motion of the pendulum bob is a nonlinear differential equation that cannot be solved in terms of elementary functions.
To describe the problem completely, it is also necessary to specify the initial state of the system.
How many initial conditions do you need? (What is the order of the differential equation?)
What are good choices for initial conditions?
The differential equation along with the initial conditions is a mathematical model for this pendulum system.