Math Model
The study of mechanical systems requires the balance of forces. Since the
system under investigation has two degrees of freedom, we should choose a
coordinate system. Making an intelligent choice will simplify the further
study.
In order to derive the equations of motion, we use Newton's second law
which says that the acceleration, a, of the mass,
m, in both the radial and the angular directions is proportional
to the net force, F, acting on it in each direction.
To apply Newton's second law, we should identify the forces acting on the
mass and show them in a Free Body Diagram (FBD).
Note that the force due to gravity can be decomposed into two parts, one in the radial direction and the other in the angular direction.
Now we can express Newton's law mathematically. We need to write F and a in terms of r, , t, l, k, m, and any necessary constants, such as the gravitational acceleration, g.
The forces acting on the mass in the radial direction are:
(restoring force of the spring + gravity)
The forces acting on the mass in the angular direction are:
(gravity)
In order to write down the equations of motion, we need to express the acceleration in polar coordinates.
Remember that the total spring stretch, r consists of two parts, the static stretch, rs, and the dynamic stretch, rd:
Now we are ready to use Newton's second law:
Combining the expressions for the total forces acting on the mass and for the acceleration in polar coordinates, we finally derive the equations of motion.
The system of equations obtained consists of two coupled non-linear differential equations of the second order, thus it is a system of fourth order.
|
What would be a wise choice for the spring-pendulum system?
|
|
Polar coordinates. Why?
|
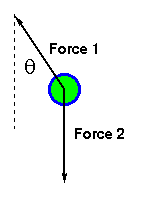
FBD |
Analysis |
|
We can write the description of the forces acting on the mass by observing
the FBD and we name: Force 1 as the restoring force of the spring Force 2 as the force due to gravity. |
Note that the force due to gravity can be decomposed into two parts, one in the radial direction and the other in the angular direction.
Now we can express Newton's law mathematically. We need to write F and a in terms of r, , t, l, k, m, and any necessary constants, such as the gravitational acceleration, g.
The forces acting on the mass in the radial direction are:
(restoring force of the spring + gravity)
The forces acting on the mass in the angular direction are:
(gravity)
In order to write down the equations of motion, we need to express the acceleration in polar coordinates.
Remember that the total spring stretch, r consists of two parts, the static stretch, rs, and the dynamic stretch, rd:
| r = rs + rd |
Now we are ready to use Newton's second law:
Combining the expressions for the total forces acting on the mass and for the acceleration in polar coordinates, we finally derive the equations of motion.
The system of equations obtained consists of two coupled non-linear differential equations of the second order, thus it is a system of fourth order.
|
To describe the problem completely, the initial state of the system is needed.
How many initial conditions do we need?
|
Copyright © 1999 Rensselaer Polytechnic Institute. All Rights Reserved.