


Next: 4 Normal Shock
Up: 3 Isentropic Flow
Previous: 3.1 Relationships for Small
 |
(26) |
The star values
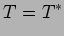 |
(31) |
The initial stagnation temperature is denoted as
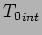 .
.
for isothermal



Next: 4 Normal Shock
Up: 3 Isentropic Flow
Previous: 3.1 Relationships for Small
Genick Bar-Meir ||| www.potto.org
copyright Dec , 2006
The pdf version is also available here
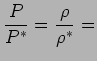 e
e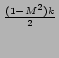
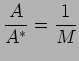 e
e
![]() .
.