 The map is decomposed in three simple operations:
The map is decomposed in three simple operations:
If we start with a small ball of initial points centered around a saddle and iterate the map the ball will be stretched and squashed along the line Wu. Similarly the small ball of initial points iterated backward in time will trace the stable separatrises. N iterations of a small circle (with radius R) around the saddle x1 are shown below.
Let stable and unstable separatrises intersect in a homoclinic point go . This point lies on stable separatrix so its orbit goes to the saddle. As since the orbit passes g1 = f(go ) then g1 belongs ws too. Under inverse iterations go orbit go to the saddle along the unstable separatrix. As since g1 = f-1(go ) then "inverse" g1 orbit go to x1 and the point lies on unstable separatrix too. So it is one more intersection of ws and wu . Therefore there are infinite number of intersections g2 , g3 ... By increasing N you can test that separatrises are very complicated. There are many intersection points and you can be entangled easy...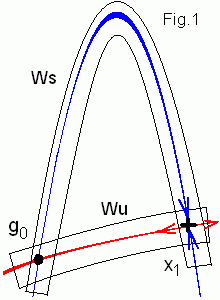 To make it a bit severe we will show that there is Smale horseshoe
in a homoclinic structure.
Let a map has a homoclinic point go . We take a region
D around the saddle. A = f ok(D) will be stretched
along unstable separatrix and reach the homoclinic point at some
k value. Similar B = f -om(D) will be stretched
along the stable separatrix and reach go . Therefore
f -o(k+m) maps A in B and makes horseshoe
as shown in the figure to the left.
Intersection points of ws and wu for
two different saddles are called heteroclinic. One can make the
horseshoe map and chaotic fractal set these points too.
To make it a bit severe we will show that there is Smale horseshoe
in a homoclinic structure.
Let a map has a homoclinic point go . We take a region
D around the saddle. A = f ok(D) will be stretched
along unstable separatrix and reach the homoclinic point at some
k value. Similar B = f -om(D) will be stretched
along the stable separatrix and reach go . Therefore
f -o(k+m) maps A in B and makes horseshoe
as shown in the figure to the left.
Intersection points of ws and wu for
two different saddles are called heteroclinic. One can make the
horseshoe map and chaotic fractal set these points too.