Бифуркации квадратичного отображения
Качественное изменение в динамике отображения при изменении параметра
называется бифуркацией.
Касательная бифуркация
При c > 1/4 итерации квадратичного отображения расходятся.
В точке c = 1/4 парабола касается диагонали, а при
c < 1/4 они пересекаются в двух точках,
соответствующих устойчивой и неустойчивой неподвижным точкам.
Это явление называется касательной бифуркацией.
Потащите параболу вниз.
Устойчивая орбита с периодом 3 также рождается в касательной бифуркации при
c = -1.75 (см. рисунок направо) и далее, при уменьшении параметра,
повторяет весь каскад бифуркаций квадратичного отображения.
Бифуркация удвоения периода
При c < -3/4 производная в левой неподвижной точке
f '(x1) = m < -1 и точка теряет устойчивость.
В окрестности c = -3/4, после первой итерации
δx' = mδx ~ -δx меняет знак, а после второй итерации
снова δx'' = m2δx ~ δx. Поэтому у
отображения появляется притягивающая периодическая орбита с периодом 2
x3 → x4 → x3 ...
Это явление называется бифуркацией удвоения периода.
У второй итерации квадратичного отображения f o2(x)
(вверху направо) при этом появляются две притягивающие неподвижные точки
x3 , x4 (соответствующие устойчивому циклу)
и неустойчивая x1 (между ними).
Отметим, что в окрестности нуля f o2(x)
похожа на параболу и при
дальнейшем уменьшении c также испытывает бифуркацию удвоения периода
после которой у квадратичного отображения появляется устойчивый цикл с
периодом 4 и т.д. То, что устойчивые орбиты с разными периодами испытывают
подобные бифуркации объясняется теорией перенормировок (renormalization theory).
Заметим, что неустойчивые орбиты уже никогда больше не исчезают.
Бифуркационная диаграмма
За динамикой вещественного квадратичного отображения удобно следить
по бифуркационной диаграмме (налево внизу).
Будем строить итерации fc: x1 = 0 →
x2 → x3 → ...→ xMaxIt для
вещественных c на плоскости (x, c). Цвета (от синего к красному)
показывают, как часто орбита попадает в данную точку.
(переходный процесс показывает, как быстро итерации сходятся).
Вы можете также проследить за орбитой точки x = 0 при
соответствующем значении c на итерационной диаграмме справа.
Управление: Щелкните мышкой, чтобы растянуть бифуркационную
диаграмму в 2 раза. Щелкните мышкой с <Ctrl> чтобы
сжать картинку. Держите <Shift>,
чтобы растянуть изображение только в c (вертикальном) направлении.
MaxIt = 2000. Координаты центра изображения x,c и
Δx,Δc
отображаются в текстовом поле. Синяя вертикальная линия проходит через
начальную точку x = 0.
Верхняя часть диаграммы начинается с касательной бифуркации при
c = 1/4. При -3/4 ≤ c ≤ 1/4 существует
единственная неподвижная притягивающая точка.
В окркстности c = -3/4 видна точка ветвления
бифуркации удвоения периода, после чего неподвижная точка теряет
устойчивость и появляется притягивающая орбита с периодом 2.
Далее после новой бифуркации удвоения
периода возникает орбита с периодом 4 и т.д.
Каскад бифуркаций удвоения периода заканчивается при c = -1.401
после чего возникает область хаотической динамики,
которая заканчивается кризисом при c = -2.
В области хаотической динамики видны узкие горизонтальные белые полосы
окон регулярнойой динамики. Самая большая полоса внизу
соответствует окну с периодом 3.
Каустики бифуркационной диаграммы
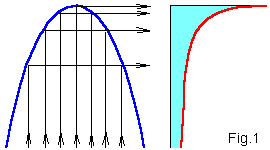 Fig.1 поясняет, что каустики в распределении точек хаотических орбит
генерируются экстремумами отображения. Поэтому особенности (выделяемые красным
цветом) на диаграмме появляются на образах критической точки
fc on(0). Обозначая gn(c) =
fcon(0), получим
Fig.1 поясняет, что каустики в распределении точек хаотических орбит
генерируются экстремумами отображения. Поэтому особенности (выделяемые красным
цветом) на диаграмме появляются на образах критической точки
fc on(0). Обозначая gn(c) =
fcon(0), получим
go(c) = 0, g1(c) = c,
g2(c) = c2 + c, ...
Кривые g0,1,...,6(c) показаны на Fig.2.
Отметим, что аттрактор квадратичного отображения заключен между
кривыми g1(c) и g2(c).
Точка пересечения каустики с вертикальной прямой x = 0 на диаграмме
соответствует окну периодической динамики.
Содержание
«Итерации квадратичного отображения
»Подобие окон регулярной динамики
изменено 3 янв 2014
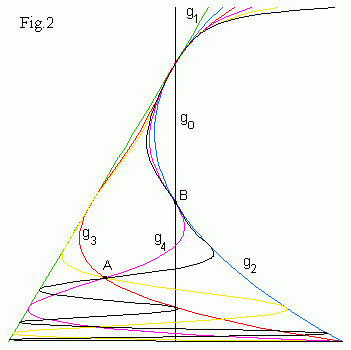
 Fig.1 поясняет, что каустики в распределении точек хаотических орбит
генерируются экстремумами отображения. Поэтому особенности (выделяемые красным
цветом) на диаграмме появляются на образах критической точки
fc on(0). Обозначая gn(c) =
fcon(0), получим
Fig.1 поясняет, что каустики в распределении точек хаотических орбит
генерируются экстремумами отображения. Поэтому особенности (выделяемые красным
цветом) на диаграмме появляются на образах критической точки
fc on(0). Обозначая gn(c) =
fcon(0), получим
