Антиферромагнетики
|
Если константа обменного взаимодействия
J < 0 , то ближайшие спины стремятся выстроиться навстречу друг
другу. Поэтому при низкой температуре в простейшем Изинговском
антиферромагнетике на квадратной решетке образуются
две упорядоченные подрешетки (расположенные как клетки на шахматной доске)
в которых спины направлены в противоположные стороны. При старте из
случайной конфигурации спинов вы можете наблюдать формирование кластеров
упорядоченной фазы и движение доменных границ.
|
В апплете приведенном внизу
использован алгоритм Метрополиса. Строится зависимость энергии и
намагниченности от марковского времени (вычисление параметра порядка вы
можете добавить сами :)
Управление Нажмите кнопку мыши, чтобы получить следующую итерацию.
Нажмите "Enter", чтобы ввести новое значение температуры T.
Забавно, что антиферромагнитное упорядочивани возникает и в алгоритме
термостата при отрицательных температурах.
Параметр порядка антиферромагнетика
Параметр порядка в простейшем антиферромагнетике определяется разностью
намагниченностей двух подрешеток L = M1
- M2 . Суммарная намагниченность M =
M1 + M2 в упорядоченной фазе мала и
энергией магнитного поля можно пренебречь. При низкой температуре
M12 = M22 =
Mo2 = const и если положить Mo = 1 ,
то L·M = 0 , L2 + M 2 =
1 . Основному состоянию отвечают L2 = 1, M = 0 .
|
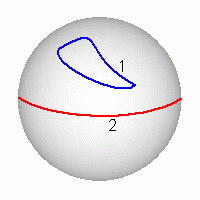
Однако, в отличие от ферромагнетика вектора L и -L
описывают одно и тоже состояние антиферромагнетика [4]. Поэтому на сфере
L2 = 1 нужно отождествить диаметрально противоположные
точки. На рисунке показаны контур 1, который стягивается в точку и
замкнутый контур 2 проходящий через две диаметрально противоположные
точки. Второй контур топологически неэквивалентен первому и поэтому в
антиферромагнетике существует топологический солитон - дисклинация.
|
Антиферромагнетики на треугольной решетке
+ - + - o
- + - + - o
+ - + o o
|
Для квадратной решетки антиферромагнитное упорядочивание Изинговского
антиферромагнетика очевидно. Однако, на треугольной решетке невозможно
разместить + и - так, чтобы на соседних узлах спины всегда
имели противоположную ориентацию (это явление называется фрустрацией).
|
Поэтому при конечных температурах на такой решетке нет фазового перехода
[1]. Он появляется, если учесть соседей следующих за ближайшими.
[1] Р.С.Гехт Магнитные состояния и фазовые переходы во
фрустированных антиферромагнетиках с треугольной решеткой.
УФН, 159(2), 261 (1989).
[2] К.Ь.Херд Многообразие видов магнитного упорядочения
в твердых телах. УФН, 142(2), 331 (1984).
[3] С.А.Никитин
Магнитные структуры в
кристаллических и аморфных веществах
[4] А.М.Косевич, Б.А.Иванов, А.С.Ковалев
Нелинейные волны намагниченности. Динамические и топологические солитоны.
(1983)
Содержание
«Фазовый переход второго рода
»Вихри в XY модели
изменено 30 мая 2004