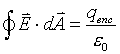
The equation
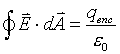
expresses Gauss's Law in integral form.

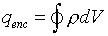
where is the charge density within the Gaussian surface. Therefore,
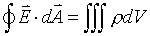
The left-hand side of this equation involves a surface integral, while the right hand side involves a volume integral.
Can the surface integral be converted to a volume integral? The answer is yes, and it is provided by the Divergence Theorem:
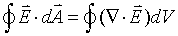
Where the divergence of  ,
,
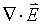 , is a scalar
function defined as
, is a scalar
function defined as
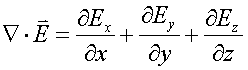
in Cartesian (rectangular) coordinates. (For more information about Cartesian coordinates, visit the glossary.)
Gauss's Law can now be written as
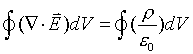
or
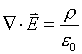
This is the statement of Gauss's Law in differential form. It constitutes one of the four Maxwell's Equations.
When you have finished here, go on to learn about what Gauss's Law has to say about magnetism.