
Previously, we defined the flux of water through a Gaussian surface by equation (4).

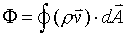
|
(4) |
Similarly, if we construct a Gaussian surface in the presence of an
electric field  , we can
define the electric flux
, we can
define the electric flux 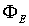 by
by
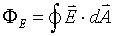
|
(6) |
The difference between water flux and electric flux is that water physically flows through the Gaussian surface, thus making water flux much easier to visualize. In the case of electric flux, we use the analogy presented by equations (4) and (6), and imagine that the electric field and its flux flow through the Gaussian surface.
The analogy between the two vectors 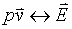 leads us to think that the electric
flux
leads us to think that the electric
flux 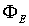 may be directly related
to its "source" via a relationship similar to equation (5).
may be directly related
to its "source" via a relationship similar to equation (5).
This relationship between the electric flux and its source or charge is indeed the statement of Gauss's Law:
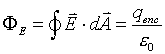
|
(7) |
The net electric flux through a Gaussian surface is proportional to the net charge enclosed within the surface.
It is important to emphasize that the charge 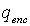 includes only the charges
within the Gaussian surface.
includes only the charges
within the Gaussian surface.
You may want to look at a not entirely rigorous proof.
Now, work with a partner on some collaborative problems.