 can be calculated using Coulomb's
Law. There are two possible methods: Calculate the field vectors due
to all the charges and then add them vectorially, or first calculate
the electric potential V due to these charges and take its
negative gradient.
can be calculated using Coulomb's
Law. There are two possible methods: Calculate the field vectors due
to all the charges and then add them vectorially, or first calculate
the electric potential V due to these charges and take its
negative gradient.
For a given charge distribution, the electric field  can be calculated using Coulomb's
Law. There are two possible methods: Calculate the field vectors due
to all the charges and then add them vectorially, or first calculate
the electric potential V due to these charges and take its
negative gradient.
can be calculated using Coulomb's
Law. There are two possible methods: Calculate the field vectors due
to all the charges and then add them vectorially, or first calculate
the electric potential V due to these charges and take its
negative gradient.
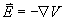
For more information on this subject, see the Electric
Potential module.
There exists an alternate method to finding the electric field, which
is provided by Gauss's Law. This "new" method
is much more elegant and powerful when there is a certain symmetry to
the physical situation--for example, when a charge distribution is
spherically symmetric.
Suppose we construct a closed surface around parts of a given charge distribution. This enclosed surface, called a Gaussian Surface, can be of any shape and size we decide. (Note that a Gaussian surface is not a physical surface, such as a plastic bag, but is a mathematical construct.)

Gauss's Law relates the electric fields on the Gaussian surface to the net charge inside it.
For instance, take the above illustration. The electric field (shown
by the vectors  is
proportional to the enclosed charges only. Therefore, only charges
q2, q3, and q5
affect the net electric field through the Gaussian surface. The other
charges have no effect!
is
proportional to the enclosed charges only. Therefore, only charges
q2, q3, and q5
affect the net electric field through the Gaussian surface. The other
charges have no effect!
Before we can formulate the exact statement of Gauss's Law, we need to introduce and discuss the concept of flux in a general way. Flux plays an important role not only in electrostatics, but also in areas such as fluid mechanics.
FLUX
The word flux is associated with something flowing. This "something" may be the water flow in a river or the mass flow in lava. Similarly, we can introduce "electric flux," visualizing the electric field vector "flowing" through a surface area.
Since it is easiest to visualize the water flowing, we will use the water flow as the prototype example in the discussion of flux.
Go on and try one such example now.