

An insulating sphere of radius R has a total charge q uniformly
distributed throughout its volume.
We want to find the electric field everywhere, that is, at an
inside point r < R, and also at an outside point
r > R.
|

|
We already know that for a spherically symmetric case,
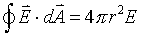 .
We have to be careful about qenc,
though. qenc is the net charge within the Gaussian
surface, not the total charge q of the entire sphere. For this
reason, we need to multiply the total charge by the ratio of the
volume of the Gaussian surface to the volume of the entire sphere:
.
We have to be careful about qenc,
though. qenc is the net charge within the Gaussian
surface, not the total charge q of the entire sphere. For this
reason, we need to multiply the total charge by the ratio of the
volume of the Gaussian surface to the volume of the entire sphere:
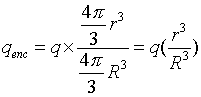
Therefore,
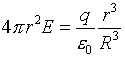
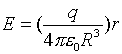
|
For the case where r > R: We construct a spherical Gaussian surface through an outside point r > R, and apply Gauss's Law. In this case, 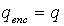
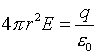
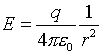
|

|
The graph below is of the magnitude of the electric field due to a uniformly charged sphere, plotted as a function of distance from the center of the sphere.

Now, practice by using a few interactive applets.