
|

|

|
Imagine that we start with a conductor of an arbitrary shape, with no
charge on it. Now we give this conductor a net charge
q--for example, by touching it momentarily with a charged
rod.

|

|

|
The charge q will spread throughout the conductor and will eventually settle down to its equilibrium distribution.
Where does the charge q reside in the conductor when it is in equilibrium? We will use Gauss's Law to prove an important property of a charged conductor in equilibrium:
In electrostatic equilibrium, the electric charge on an isolated conductor resides entirely on its surface. No charge is found within the body of the conductor.
Proof using Gauss's Law:

Construct a Gaussian surface just inside the surface of the
conductor. By definition, an equilibrium situation is reached when the
charges are arranged so that they no longer move within the
conductor. That is, there is no electric field within the conductor
at equilibrium. (If there were an electric field, it would cause
the charges to move.) Therefore, the electric flux 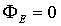 about this Gaussian
surface. But Gauss's Law says that
about this Gaussian
surface. But Gauss's Law says that 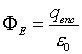 , so the enclosed charge
qenc = 0. One can make the Gaussian surface approach
as close to the conductor surface as possible, and the enclosed charge
is still zero. Therefore, the only place that the given charge
q can reside is on the conductor's surface.
, so the enclosed charge
qenc = 0. One can make the Gaussian surface approach
as close to the conductor surface as possible, and the enclosed charge
is still zero. Therefore, the only place that the given charge
q can reside is on the conductor's surface.
To test your understanding, try out this practice problem.