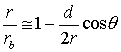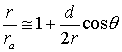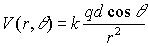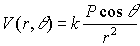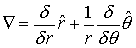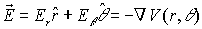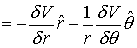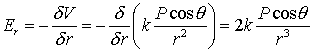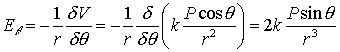Electric Dipole Field
When the separation distance "d" between two opposite point charges
in the previous page is small compared to the distance from the center
of the two charges to the observation point P, the system is called an
electric dipole. The field it produces is called the electric dipole
field and it has many applications - for example, in the dielectric
properties of matter.
Potential from a Dipole

Figure 1
Assume that the electric dipole is located as shown in the above
figure, and we want to calculate the potential and the electric field
it produces at point P. We specify the location of P in polar
coordinates as (r, q)
|
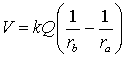
|
(15)
|
|
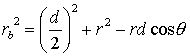
|
(16)
|
|
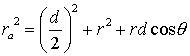
|
(17)
|
Using the Law of Cosines, we can rewrite equation 16:
|
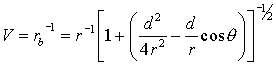
|
(16a)
|
Notice that the quantity in the square brackets is in the form
[1+x]-1/2, where
X is a quantity much smaller than 1, because the separation distance
is much smaller than the distance
r to the observation point.
We can then expand [1+x]
-1/2 by using a
Taylor Series:
Then equation 16a becomes
It is in the nature of dipole approximations that
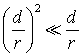 Therefore, it
is a good approximation to retain up to the linear term in d/r:
Therefore, it
is a good approximation to retain up to the linear term in d/r:
|
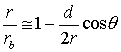
|
(18)
|
Similarly,
|
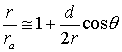
|
(19)
|
Substituting equations 18 and 19 into equation 15, we obtain
The product of charge and the separation distance is called the
Electric Dipole Moment. It is given by P = qd. This quantity appears
often in the study of dipoles and dielectric materials.
|
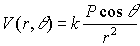
|
(20)
|
Electric Field from a Dipole
In polar coordinates, the gradient operator is
Therefore,
|
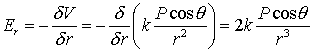
|
(21a)
|
|
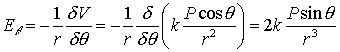
|
(21b)
|
The equipotential lines and the electric field lines due to a dipole can
be seen in figure 2 below, where the separation distance d is small compared
to the observation distance.
Next, you should move on the explore an electric dipole using our
Field Applet. You may also take a look at one
of the many applications
of electric dipoles.
Copyright
1998-2000
Rensselaer Polytechnic Institute. All Rights Reserved.

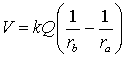
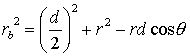
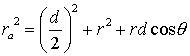
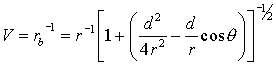
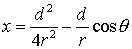
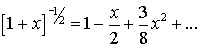
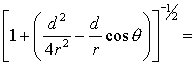
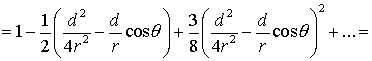
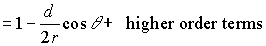
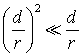 Therefore, it
is a good approximation to retain up to the linear term in d/r:
Therefore, it
is a good approximation to retain up to the linear term in d/r: