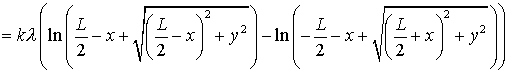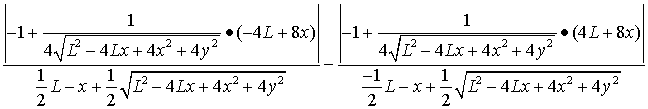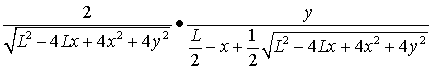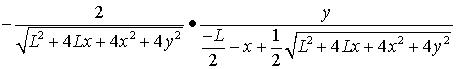Rather than restricting ourselves to being along the axis of a line of charge, let's look at the situation where we can be anywhere. The general scheme of the situation is as follows:
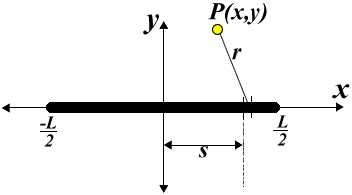

Give an expression for the potential V, at an arbitrary
point P, in terms of x and y.
Answer
|
| (24a) |
|
| (24b) |
This potential is shown below as an equipotential plot (contour plot) and a 3-dimensional bar plot.
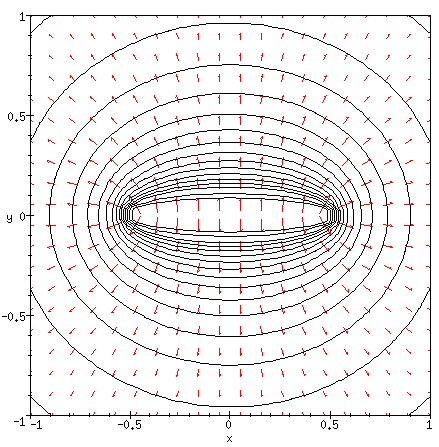
Equipotential surfaces due to a line charge.
Three-dimensional plot of potential due to a line charge.
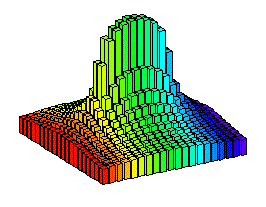
The colors are for illustration only - they have no physical meaning.
The electric field E is given by equation (1):
|
| (25a) |
|
| (25b) |
|
| (25b, cont.) |
The electric field components (25a) and (25b) are shown below:
Ex as a function of x at y = 0.01 m. As in the line charge example, L = 1 m and Q = 0.1 C.
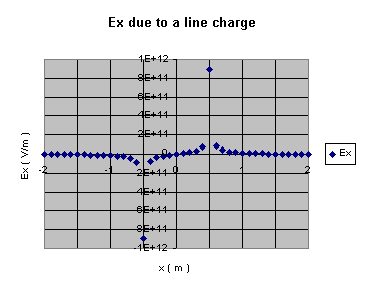
Notice that at this small value of y (0.01 m is much smaller than L = 1 m), Ex behaves very much like the field calculated along the axis in the line charge example. Also notice that Ex peaks at both ends of the line charge.
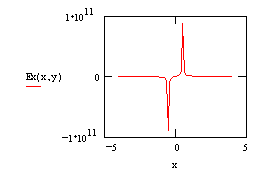
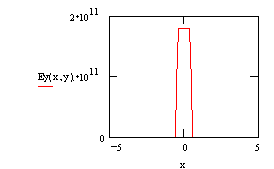
Electric field components as a function of x at y = 0.01 m, L = 1 m, and l = 0.1 C/m Lambda is linear charge density.
Go to the Collaborate page and think about how point charges become line charges.