Answer to Problem 56
Use the above result to rewrite the equation (6.2):
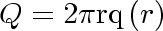
Equation 82

Equation 83
Using equation (6.1) to substitute for
 , we obtain the
differential equation as follows.
, we obtain the
differential equation as follows.
Since

Equation 84
then

Equation 85
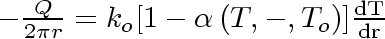
Equation 86
Let

Equation 87
Then

Equation 88
NOTE: Equation (6.3),
together with the boundary temperatures
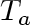 and
and
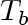 at
at
 and
and
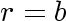 ,
respectively, define the boundary value
problem
,
respectively, define the boundary value
problem
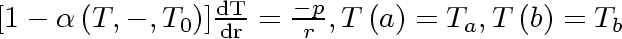
Equation 89
in which the constants
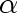 ,
,
 ,
,
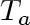 ,
and
,
and 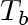 are given and the constant
are given and the constant
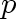 is to be determined along with the solution
is to be determined along with the solution
 .
The BVP above is solved in Problems 6.2, 6.3, and 6.4.
.
The BVP above is solved in Problems 6.2, 6.3, and 6.4.
Generally, two boundary conditions arise in conjunction with a second order ordinary differential equation (ODE). But equation (6.3) is a first order ODE which usually has a single associated boundary condition to fix the arbitrary constant of integration.
The additional boundary condition is needed to
determine the value of
 .
.