Answer to Problem 26
Setting
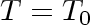 when
when
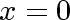 gives
gives
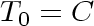 . Then, since
. Then, since
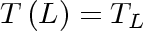 ,
we have
,
we have
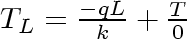
Equation 12
or
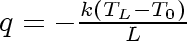
Equation 13
Finally substituting
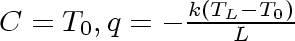
Equation 14
in the expression for
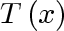 , we obtain
, we obtain
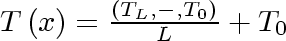
Equation 15
It should be noticed that when
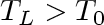 ,
,
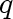 is negative; this is consistent with our intuition
that heat flows from higher to lower temperatures.
is negative; this is consistent with our intuition
that heat flows from higher to lower temperatures.
Note too that the temperature distribution is a
linear function of
 .
.
Finally, to underscore the role of the gradient in
this analysis, it is readily verified that the
expressions for
 and
and
 given by equations (3.4) and (3.5) satisfy
(1.1),
Fourier's law of heat conduction.
given by equations (3.4) and (3.5) satisfy
(1.1),
Fourier's law of heat conduction.